LÓGICA QUANTICA: UMA INTRODUÇÃO

LÓGICA QUÂNTICA

UMA INTRODUÇÃO
HISTÓRICO-FILOSÓFICA

(AVISO: É muito importante que para a leitura deste texto, você já tenha acompanhado os textos de lógica proposicional (1-2) e lógica modal (1-2).)

PREFÁCIO

O Quantum Logic (QL) foi desenvolvido como uma tentativa de construir uma estrutura proposicional que permita descrever os eventos de interesse em Quantum Mechanics (QM). QL substituiu a estrutura booleana, que, embora apropriada para o discurso da física clássica, era inadequada para representar o reino atômico. A estrutura matemática da linguagem proposicional sobre sistemas clássicos é um conjunto de energia, parcialmente ordenado pela inclusão do conjunto, com um par de operações que representam conjunção e disjunção. Esta álgebra é consistente com o discurso sobre fenômenos clássicos e relativistas, mas inconsistente em uma teoria que proíbe, por exemplo, dar valores de verdade simultâneos às seguintes proposições: "O sistema possui essa velocidade" e "O sistema está neste lugar.

Durante o seu desenvolvimento, a QL começou a se referir não apenas a uma lógica, mas também às múltiplas linhas de pesquisa que tentaram entender QM de uma perspectiva lógica. Este artigo fornece um mapa dessas múltiplas abordagens para apresentar as estratégias e problemas muito diferentes discutidos na literatura QL. Quando possível, são evitadas fórmulas desnecessárias para dar uma compreensão intuitiva dos conceitos antes de derivar ou introduzir a matemática associada. No entanto, para aqueles leitores que desejam se envolver mais profundamente com o assunto da QL, o artigo fornece uma bibliografia extensa.

1. Lógica e Física

QL relaciona as duas disciplinas aparentemente diferentes da física e da lógica. Essas disciplinas têm sido intimamente relacionadas desde sua origem. Foi Aristóteles que criou a lógica clássica e a usou para desenvolver seu próprio esquema físico e metafísico, fornecendo uma resposta ao problema do movimento e do conhecimento estabelecido pelas escolas de pensamento heráclitas e eleáticas. O movimento foi então considerado por Aristótelesem termos de seu esquema ilimórfico, como o caminho de um potencial (indeterminado, contraditório e não idêntico) para um reino real (determinado, não contraditório e idêntico) da existência. A noção de entidade caracterizou-se por três principais princípios lógicos e ontológicos: o Princípio da Existência (PE), que permitiu a Aristóteles reivindicar a existência sobre o que é predicado, o Princípio da Não-Contradição (PNC), que lhe permitiu argumentar o que existe possui propriedades não contraditórias e o Princípio da Identidade (PI), o que lhe permitiu afirmar que o fato predicado é "o mesmo" ou permanece idêntico a si mesmo, através do tempo. A arquitetonista de Aristóteles determinou o destino da física clássica e medieval, bem como a metafísica. A transformação da ciência medieval para a ciência moderna coincide com a abolição do esquema metafísico aricalista hilomórfico como base do conhecimento. No entanto, a estrutura básica de seu esquema metafísico e sua lógica continuaram a ser a base para um raciocínio correto. Conforme observado por Karin Verelst e Bob Coecke:

Afastando a metafísica aristotélica, ao mesmo tempo que continua a usar a lógica aristotélica como um "aparelho de raciocínio" vazio, implica, portanto, perder a possibilidade de explicar a mudança e o movimento em qualquer descrição do mundo que se baseie nela. O fato de que a lógica aristotélica se transformou durante o século XX em diferentes sistemas lógicos axiomáticos formais utilizados na filosofia e na ciência de hoje realmente não importa, porque o princípio fundamental e, portanto, a ontologia fundamental, permaneceu o mesmo ([40], p. xix). Essa lógica "esvaziada" contém realmente uma ontologia eleática, que permite apenas descrições estáticas do mundo. [231, p. 173]

Foi Isaac Newton, que foi capaz de traduzir em um formalismo matemático fechado tanto os pressupostos ontológicos presentes na lógica aristotélica (Eleática) quanto o ideal materialista de "res extensa", juntamente com a realidade como seu modo de existência. O termo "real" refere-se aqui à preexistência (dentro da representação transcendente) e não à observação hic et nunc. Todo sistema físico pode ser descrito exclusivamente por meio de suas propriedades reais. A mudança do sistema pode ser explicada pela mudança de suas propriedades reais. As propriedades potenciais ou possíveis só são consideradas como os pontos a que o sistema pode chegar em um futuro instante de tempo. Como diz Dennis Dieks: "Na física clássica, a descrição mais fundamental de um sistema físico (um ponto no espaço de fase) reflete apenas o real e nada que é meramente possível. É verdade que, por vezes, estados envolvendo probabilidades ocorrem na física clássica: pense nas distribuições de probabilidade ρem mecânica estatística. Mas a ocorrência de possibilidades em tais casos apenas reflete nossa ignorância sobre o que é real. Os estados estatísticos não correspondem aos recursos do sistema real, mas quantificam nossa falta de conhecimento sobre esses recursos reais ". [98, p. 124-125] No entanto, no QM, a estrutura diferente das propriedades físicas do sistema determina uma mudança de natureza quanto ao significado de possibilidade e potencialidade. Na verdade, QM tem sido relacionado à modalidade desde 1926, quando Max Born interpretou a função da onda quântica Ψ em termos de uma densidade de probabilidade. No entanto, ficou claro desde o início que esta nova possibilidade quântica era algo completamente diferente do que se pensava nas teorias clássicas.

[O] conceito da onda de probabilidade [na mecânica quântica] era algo inteiramente novo na física teórica desde Newton. Probabilidade em matemática ou em mecânica estatística significa uma declaração sobre nosso grau de conhecimento da situação atual. Ao jogar dados, não conhecemos os detalhes finos do movimento das nossas mãos que determinam a queda dos dados e, portanto, dizemos que a probabilidade de jogar um número especial é apenas uma em cada seis. A função de onda de probabilidade, no entanto, significou mais do que isso; Isso significava uma tendência para algo. [152, p. 42]

De acordo com Werner Heisenberg, o conceito de onda de probabilidade "foi uma versão quantitativa do antigo conceito de" potenciala "na filosofia aristotélica. Introduziu algo em pé no meio entre a idéia de um evento e o evento real, um estranho tipo de realidade física, no meio entre possibilidade e realidade ". [152, p. 42] Na verdade, contrariamente à possibilidade clássica que apenas se refere ao nosso conhecimento incompleto de um estado real de coisas, as possibilidades quânticas interagem entre si. Esse fato, completamente estranho às teorias clássicas, é explorado por desenvolvimentos tecnológicos atuais no processamento de informações quânticas, por exemplo, computação quântica, criptografia quântica, teletransporte quântico. Contudo, para além desta questão muito fundamental sobre o domínio da existência que a estrutura lógica do QM nos obriga a considerar, há muitos outros aspectos que têm sido objeto de discussão na literatura desde a origem do QM. De fato, a interpretação do postulado quântico de Planck, o princípio da superposição, a não comutação de observáveis ​​ou a identidade de partículas quânticas - apenas para mencionar alguns problemas importantes que nos ajudam a considerar de forma coerente o que a QM está falando . QL tem sido uma ferramenta importante para discutir todos esses assuntos fascinantes. a não-comutatividade de observáveis ​​ou a identidade de partículas quânticas - apenas para mencionar alguns problemas importantes que nos ajudam a considerar coerentemente o que QM está falando. QL tem sido uma ferramenta importante para discutir todos esses assuntos fascinantes. a não-comutatividade de observáveis ​​ou a identidade de partículas quânticas - apenas para mencionar alguns problemas importantes que nos ajudam a considerar coerentemente o que QM está falando. QL tem sido uma ferramenta importante para discutir todos esses assuntos fascinantes.

2. A Estrutura Lógica da Mecânica Quântica

Em termos lógicos, a mecânica newtoniana pode ser descrita através da "lógica de uma mente onisciente em um universo determinista" [54] porque, em tal universo, qualquer afirmação é decidida semanticamente. Ou seja, qualquer proposição p ou sua negação ¬ p é verdadeira (princípio de princípio excluído), ambas as afirmações p e ¬ pnão pode ser simultaneamente verdadeiro (PNC), os significados são nítidos e inequívocos eo significado de uma expressão composta é determinado pelos significados de suas partes. Do ponto de vista matemático, tanto os aspectos sintáticos quanto os semânticos da lógica proposicional clássica podem ser completamente descritos em termos de álgebra booleana. No entanto, a estrutura do QM não se encaixa nesses recursos. O principal motivo disso é que, nas teorias físicas, a informação sobre o estado dos assuntos está codificada no que é chamado de "estado físico". Tanto no clássico quanto no QM existem estados de conhecimento máximo, mas as implicações lógicas que podem ser compreendidas a partir de cada situação não é a mesma. Enquanto na mecânica clássica, a informação máxima sobre uma situação implica integridade lógica, o que significa que toda afirmação sobre a situação representada pelo estado é verdadeira ou falsa, na QM um estado não pode decidir a verdade ou a falsidade de todas as proposições sobre eventos. Isso ocorre porque existem estados relacionados com uma propriedade e sua negação chamada "estados de superposição".

Na física clássica, cada sistema pode ser descrito especificando suas propriedades reais. Matematicamente, isso acontece representando o estado de um sistema de massa m por um ponto ( p, q ) em seu espaço de fase correspondente Γ de posições q e momenta p . A lei de Newton nos diz como esse ponto se move ao longo do caminho determinado pelas condições iniciais. As magnitudes físicas são representadas por funções reais sobre Γ. Essas funções se repitam entre si e podem ser interpretadas como todas possuindo valores definidos a qualquer momento, independentemente das observações físicas. Os eventos físicos são representados por subconjuntos de Γ. O conjunto de potência ℘ de Γ dotado de operações teóricas definidas: interseção (∩),union(∪) e set-complemento originam uma álgebra booleana. Interpretando essas operações como conectivos lógicos, representam e (∧), ou (∨) e não (¬). A ligação entre a estrutura algebraica da mecânica clássica e a lógica clássica é óbvia. Ao lidar com muitos graus de liberdade, uma descrição estatística é útil. A estrutura lógica-algébrica associada à mecânica clássica admite a definição de uma medida de probabilidade sobre ela com seus elementos considerados como eventos. A probabilidade resultante é uma probabilidade clássica de Kolmogorovian.

De acordo com a axiomatização de QM de John von Neumann, a interpretação matemática de um sistema físico é um complexo espaço Hilbert separável H, e um estado puro é representado por um raio em H. Diferentemente do esquema clássico, as magnitudes físicas são representadas por auto-adjuntos operadores em H que, em geral, não se deslocam sob a multiplicação. Os valores que qualquer magnitude pode tomar são os autovalores do operador correspondente, cada um dos quais vem com o seu equivalente. A não comutatividade dos operadores tem conseqüências interpretativas problemáticas, pois é então difícil afirmar que as magnitudes quânticas assim representadas são simultaneamente pré-existentes para a observação. A evolução do estado é dada pela equação de Schrödinger que, devido à sua linearidade, implica a existência formal de superposições quânticas de estados. O fato de que os estados podem ser combinados linearmente proíbe o uso de meros subconjuntos como representantes de proposições, eles são bem representados por subespaços fechados de H.

Historicamente, a primeira abordagem de uma idéia de QL é no Capítulo 3 do livro de von Neumann sobre a formulação matemática de QM [234], onde relaciona operadores lineares, nomeadamente as projeções sobre o espaço espacial H, com os representantes de "proposições experimentais" afiliadas com o sistema: "[...] a relação entre as propriedades de um sistema físico, por um lado, e as projeções, por outro, possibilita uma espécie de cálculo lógico com estes". De fato, os subespacios fechados estão em um uma correspondência de um a um com os projetores sobre eles: "Se apresentarmos, juntamente com as projeções E , o coletor linear fechado R que pertence a eles ( E = P R), então os coletores lineares fechados correspondem igualmente às propriedades de S [S é o sistema]. "[234, p. 250] O conjunto de subespaços fechados de H, ordenados por inclusão e equipados com definições adequadas de operações algébricas, dá origem a uma rede [180], ou seja, um conjunto parcialmente ordenado (L , ∨ , ∧) em que cada par de elementos tem um supremo chamado juntar (∨) e um ínfimo chamado meet (∧) que satisfazem:

1. leis comutativas para as operações de reunião e junção: x ∨ y = y ∨ x , x ∧ y = y ∧ x
2. leis de absorção: x ∨ ( x ∧ y ) = x , x ∧ ( x ∨ y ) = x
3. leis associativas: x ∨ ( y ∨ z ) = ( x ∨ y ) ∨ z , x ∧ ( y ∧ z ) = ( x ∧ y ) ∧ z

A rede pode ter um máximo (ou superior) 1, que é a identidade para a operação ∧ e um mínimo (ou inferior) 0, a identidade para a operação ∨. É dito que uma rede (L , ∨ , ∧ , 1 , 0) é modular quando, para todos os elementos x , y e z , se x ≤ z , então

x ∨ ( y ∧ z ) = ( x ∨ y ) ∧ z

Um orthocomplement x ⊥ do elemento x é definido de tal forma que eles satisfazem:

1. a lei do complemento: x ⊥ ∨ x = 1 e x ⊥ ∧ x = 0
2. a lei de involução: x ⊥⊥ = x
3. a lei de reversão de ordem: se x ≤ y então y ⊥ ≤ x .

A rede modular é chamada ortomodular se estiver equipada com uma instalação ortográfica. A rede de subespaços de H, denotada por L (H), é chamada de rede de Hilbert associada a H e motiva a QL padrão [41].

Esta é a proposta de Garret Birkhoff e J. von Neumann para a estrutura algébrica que organiza as proposições da linguagem da QM. Esta é uma estrutura bastante diferente da clássica. Na verdade, como mencionado acima, na lógica clássica das proposições organizar-se no poder definir com operações ∧, ∨ e ¬ representando os conectivos linguagem clássica e , ou e não . Esta estrutura constitui uma álgebra booleana que satisfaz as leis distributivas de e e ou :

( x ∧ y ) ∨ z = ( x ∧ z ) ∨ ( y ∧ z )

( x ∨ y ) ∧ z = ( x ∨ z ) ∧ ( y ∨ z )

Os subespacios fechados do espaço de Hilbert H formam uma álgebra chamada uma rede de Hilbert denotada como L (H). Em qualquer treta de Hilbert, a operação de reunião ∧ corresponde à interseção teórica estabelecida entre subespaços e a operação de junção ∨ corresponde ao menor subespaço fechado de H contendo a união teórica definida de subespaços. Desta forma, a relação de ordem ≤ associada à rede corresponde à inclusão set-teórica de subespaços. Note-se que L (H) é uma rede limitada onde H é o máximo, denotado por 1, eo subespaço vazio é o mínimo, denotado por 0. Esta rede equipada com a relação do complemento ortogonal ⊥ pode ser descrita como uma orto - eletrônica [162 ].

3. Origem da lógica quântica

O nascimento oficial de QL foi produzido com o trabalho seminal de 1936 "A lógica da mecânica quântica", onde Birkhoff e von Neumann apresentaram a proposta de uma lógica não clássica para a teoria, argumentando que o problema de se o formalismo espacial de Hilbert mostrava um A estrutura lógica pode ser útil para a compreensão da QM. Na introdução ao trabalho, eles fazem questão:

Um dos aspectos da teoria quântica que atraiu a atenção mais geral é a novidade das noções lógicas que ela pressupõe. Afirma que mesmo uma descrição matemática completa de um sistema físico S não permite, em geral, prever com certeza o resultado de uma experiência em S, e que, em particular, nunca pode prever com certeza tanto a posição quanto o momento de S(Princípio da incerteza de Heisenberg). Afirma ainda que a maioria dos pares de observações não podem ser feitas em S simultaneamente (Princípio de Não Comutatividade de Observações). [...] O objeto do presente artigo é descobrir qual estrutura lógica se pode esperar encontrar em teorias físicas que, como a mecânica quântica, não estão de acordo com a lógica clássica. [41]

Como dito acima, a estrutura proposicional que deu origem a QL foi o ortholattice <L (H) , ∨ , ∧ , ⊥ ,1 , 0>. Os diferentes caracteres propostos para os representantes dos conectivos lógicos mudam completamente o significado desses conectivos. Uma característica relevante do ∨ é que, diferentemente do caso na semântica clássica, uma disjunção quântica pode ser verdadeira, mesmo que nenhum dos membros seja verdadeiro. Isso reflete, por exemplo, o caso em que estamos lidando com um estado como o de um spin 1 / 2 sistema que está em uma combinação linear de estados -se e para baixo. Ambas as proposições, "o estado é" e "o estado está baixo", pode não ter um valor de verdade definido (o princípio do meio excluído é violado), mas a disjunção "o estado está em alta ou o estado está para baixo" é uma tautologia. O caráter distintivo da estrutura é o fracasso da lei distributiva, uma lei que mantém na lógica clássica. Isso significa que se p , q e r são proposições,

x ∧ ( y ∨ z ) ≠ ( x ∧ y ) ∨ ( x ∧ z )

Birkhoff e von Neumann observaram esse fato em seu artigo: "[...] Considerando que os lógicos geralmente assumiram que as propriedades da negação eram as menos capazes de suportar uma análise crítica, o estudo da mecânica aponta para as identidades distributivas como as mais fracas link na algebra da lógica ". E concluiu que" o cálculo proposicional da mecânica quântica tem a mesma estrutura que uma geometria projetiva abstrata ". Contudo, L (H) satisfaz um tipo de distribuição fraca. No caso de um espaço Hilbert de dimensões finitas H, a ortoatologia L (H) é modular, isto é, satisfaz a seguinte condição conhecida como lei modular :

x ≤ y  ⟹ x ∨ ( y ∧ z ) = y ∧ ( x ∨ z )

A lei modular é equivalente à identidade ( x ∧ y ) ∨ ( y ∧ z ) = y ∧ (( x ∧ y ) ∨ z ). No caso de um espaço de Hilbert de dimensão infinita, a lei modular não está satisfeita. Em 1937, Kodi Husimi [156] mostrou que uma lei mais fraca, a chamada lei ortomodular é satisfeita no ortholattice L (H). A lei ortomodular diz:

x ≤ y  ⟹ x ∨ ( x ⊥ ∧ y ) = y

e é equivalente à identidade x ∨ y = (( x ∨ y ) ∧ y ⊥ ) ∨ y [180]. Este é um ponto importante para definir uma medida de probabilidade que pode ser interpretada em termos de frequências relativas (ver, por exemplo, [210, cap. 7]). Mas, ao levar os elementos de rede como eventos, isso não é possível. Josef Maria Jauch observou que:

Birkhoff e von Neumann [...] tentaram justificar a modularidade ao apontar que em redes finitas modulares pode-se definir uma função de dimensão [...] Tal função possui as propriedades características de uma medida de probabilidade e d ( a ) representaria a probabilidade a priori de encontrar o sistema com propriedade a quando nada for especificado quanto à sua preparação. Sabe-se que existem sistemas para os quais tal probabilidade a priori não existe. [159, p. 83]

Uma vez que a rede de subespacios (ou operadores de projeção) L (H) não era, em geral, modular, excluindo uma ótima definição de probabilidade (ver, por exemplo, [210, Ch. 7] e [212]) - von Neumann abandonou o Hilbert estrutura espacial para a formulação de QM e voltou-se para o estudo de anéis de operadores, que por sua vez geraram as álgebras de von Neumann [235].

Antes de discutir o desenvolvimento histórico, deve-se dizer que o nome "lógica quântica" é um pouco enganador. Como Dalla Chiara et al. observação: "pela lógica quântica padrão, geralmente se usa a rede ortomodular completa com base nos subespaços fechados em um espaço de Hilbert. Não é necessário observar que uma terminologia que identifique uma lógica com um exemplo particular de uma estrutura algébrica se torne um pouco enganosa do ponto de vista lógico rígido ". [78] Diferentes formas de QL podem ser construídas através da construção de semânticas algébricas ou Kripkeanas sobre a estrutura algébrica do espaço de Hilbert (ver, por exemplo, [81]).

4. Lógica quântica em perspectiva histórica e filosófica

QL tem sido um campo de debate em filosofia, bem como a física quântica. Dentro da QL, muitas abordagens filosóficas e linhas de pesquisa diferentes foram desenvolvidas, discutidas e abordadas. Do neo-Kantismo ao empirismo e ao realismo aristotélico, a pesquisa lógica quântica abriu a porta para um dos debates mais interessantes em física e filosofia da física na segunda metade do século passado. No entanto, embora existam muitas perspectivas diferentes em relação à QL, pode-se caracterizar sua característica interpretativa mais geral em termos de uma atitude estrategicamente subversiva em relação à lógica clássica e os próprios fundamentos da compreensão metafísica. A este respeito, a fim de esclarecer o vasto mapa de interpretações sobre QM e descobrir o significado físico da teoria, pode-se considerar as estratégias que os diferentes intérpretes tomaram. Enquanto o primeiro grupo partiu de um conjunto de pressupostos metafísicos (clássicos) e pretendia mudar o formalismo para encaixar QM na imagem metafísica desejada [por exemplo, a mecânica bohmiana, a teoria Ghirardi-Rimini-Weber], um segundo grupo concentrou sua esforços - tomando como ponto de vista o formalismo ortodoxo - na tentativa de compreender as simetrias e características do formalismo, a fim de obter uma interpretação adequada da teoria. Muito mais aberto a um desenvolvimento metafísico original que nos permita entender como é o mundo de acordo com QM, QL - além de algumas pequenas exceções - é claramente parte do último grupo. Enquanto o primeiro grupo partiu de um conjunto de pressupostos metafísicos (clássicos) e pretendia mudar o formalismo para encaixar QM na imagem metafísica desejada [por exemplo, a mecânica bohmiana, a teoria Ghirardi-Rimini-Weber], um segundo grupo concentrou sua esforços - tomando como ponto de vista o formalismo ortodoxo - na tentativa de compreender as simetrias e características do formalismo, a fim de obter uma interpretação adequada da teoria. Muito mais aberto a um desenvolvimento metafísico original que nos permita entender como é o mundo de acordo com QM, QL - além de algumas pequenas exceções - é claramente parte do último grupo. Enquanto o primeiro grupo partiu de um conjunto de pressupostos metafísicos (clássicos) e pretendia mudar o formalismo para encaixar QM na imagem metafísica desejada [por exemplo, a mecânica bohmiana, a teoria Ghirardi-Rimini-Weber], um segundo grupo concentrou sua esforços - tomando como ponto de vista o formalismo ortodoxo - na tentativa de compreender as simetrias e características do formalismo, a fim de obter uma interpretação adequada da teoria. Muito mais aberto a um desenvolvimento metafísico original que nos permita entender como é o mundo de acordo com QM, QL - além de algumas pequenas exceções - é claramente parte do último grupo. um segundo grupo concentrou seus esforços - tomando como ponto de vista o formalismo ortodoxo - na tentativa de compreender as simetrias e características do formalismo, a fim de obter uma interpretação adequada da teoria. Muito mais aberto a um desenvolvimento metafísico original que nos permita entender como é o mundo de acordo com QM, QL - além de algumas pequenas exceções - é claramente parte do último grupo. um segundo grupo concentrou seus esforços - tomando como ponto de vista o formalismo ortodoxo - na tentativa de compreender as simetrias e características do formalismo, a fim de obter uma interpretação adequada da teoria. Muito mais aberto a um desenvolvimento metafísico original que nos permita entender como é o mundo de acordo com QM, QL - além de algumas pequenas exceções - é claramente parte do último grupo.

a. O Caminho Lógico Neo-Kantiano

Conforme recordado por Heisenberg em Física e Filosofia [152], a preocupação com a objetividade e o uso da linguagem comum para conceitos quânticos foi um foco importante de discussão durante o desenvolvimento da teoria:

O problema mais difícil, no entanto, sobre o uso do idioma surge na teoria quântica. Aqui não temos, no início, um guia simples para correlacionar os símbolos matemáticos com conceitos de linguagem comum e a única coisa que sabemos desde o início é o fato de que nossos conceitos comuns não podem ser aplicados à estrutura dos átomos. [...] A análise pode agora ser levada a cabo de duas formas totalmente diferentes. Podemos perguntar qual idioma sobre os átomos realmente se desenvolveu entre os físicos nos trinta anos transcorridos desde a formulação do QM. Ou podemos descrever as tentativas de definir uma linguagem científica precisa que corresponda ao esquema matemático. Em resposta à primeira questão, pode-se dizer que o conceito de complementaridade introduzido por Bohr na interpretação da teoria quântica encorajou os físicos a usar uma linguagem ambígua e não uma linguagem inequívoca. [152, p. 153]

Formulando críticas para este uso, Heisenberg argumenta que: "parece bastante duvidoso se uma expectativa [referente ao uso de conceitos clássicos] deve ser chamada de objetivo". Uma abordagem diferente, iniciada por Birkhoff e von Neumann e continuada por Carl Friedrich von Weizsäcker em os cinquenta, seria "definir uma linguagem precisa e diferente que segue padrões lógicos definidos de acordo com o esquema matemático". Carl Friedrich von Weizsäcker, assim como Hans Reichenbach [208], fizeram isso modificando o princípio do meio excluído. Como este princípio é usado na conversa diária, von Weizsäcker propôs distinguir diferentes níveis de linguagem: um nível referente a objetos, um segundo nível a declarações sobre objetos, um terceiro nível a declarações sobre declarações sobre objetos e assim por diante. A modificação da lógica clássica tem que se referir, antes de mais, ao nível dos objetos. Como o estado de um sistema nos permite prever com alguma probabilidade as diferentes propriedades que ele poderia possuir, von Weizsäcker introduziu o conceito de "graus de verdade". Para cada par de propriedades, a questão da sua verdade não é decidida. Mas "não é decidido" não é, de modo algum, equivalente a "desconhecido". Esse tipo de lógica valiosa pode ser estendida aos níveis sucessivos de linguagem.

Como observa Heisenberg, não é claro, a primeira vista, qual tipo de ontologia sustentaria esses padrões lógicos modificados; A principal preocupação no projeto de encontrar um sistema lógico associado à estrutura algébrica da teoria. Von Weizsäcker avançou esta abordagem a partir da ideia da física reconstruir em termos de sim-não-alternatives, chamado ur -alternatives (a partir do prefixo alemão 'Ur': original) e estabelecendo uma ligação entre as estruturas quântica e a estrutura do espaço-tempo. estes ur-alternativos são considerados os objetos fundamentais em física a partir dos quais, em princípio, qualquer objeto físico pode ser construído. Assim, a partir de uma noção relacionada à informação, um turno é feito para a noção de objeto físico: os objetos são reduzidos ou mesmo "feitos de" informações [178]. Posteriormente, também Holger Lyre argumentaria a favor desta possibilidade:

Na teoria quântica em particular, essa visão tem muita plausibilidade. Os objetos quânticos são representados em termos de seus espaços de estado de Hilbert, seus estados quânticos correspondem a alternativas empiricamente decidíveis. Qualquer objeto quântico pode ser ainda decomposto ou incorporado no produto tensor de dois objetos, hoje chamados de bits quânticos ou qubits. Urs, portanto, não são mais que qubits. [178]

Na década de setenta, Pieter Mittelstäedt, estudante de Heisenberg e von Weizsäcker, continuou a pesquisa QL enquadrada na tradição neo-kantiana [48]. Ao contrário da física clássica, onde todas as proposições sobre um sistema podem ser fundamentadas em conjunto, as propriedades quânticas podem ser atribuídas valores apenas em uma maneira contextual [167], proibindo assim uma interpretação em termos de substância. De acordo com este ponto de vista, a categoria de substância só pode ser aplicada a observáveis ​​compatíveis; isto é, no caso em que o estado do sistema é tal que esses observáveis ​​podem ser atribuídos valores definidos. A lógica clássica, por sua vez, permite valores de verdade para todas as proposições e, portanto, não é adequada para proposições sobre um sistema quântico, onde o conteúdo empírico das proposições é relevante ao aplicar as regras da lógica. Com o pressuposto de que as leis da lógica deveriam ser universalmente válidas, a Mittelstäedt voltou-se para buscar uma base de lógica diferente que permitisse que as provas fossem independentes do conteúdo empírico das declarações. Primeiro, ele chamou a atenção para o fato de que a compatibilidade entre duas proposições está implícita na lógica clássica. Então, a partir de proposições elementares que afirmam que um sistema possui uma determinada propriedade, que pode ser avaliada testando a propriedade em uma experiência, o conceito de diálogo foi introduzido. Vários tipos de proposições compostas podem ser definidas especificando o diálogo-jogo. Ao adicionar um Ele chamou a atenção para o fato de que a compatibilidade entre duas proposições está implícita na lógica clássica. Então, a partir de proposições elementares que afirmam que um sistema possui uma determinada propriedade, que pode ser avaliada testando a propriedade em uma experiência, o conceito de diálogo foi introduzido. Vários tipos de proposições compostas podem ser definidas especificando o diálogo-jogo. Ao adicionar um Ele chamou a atenção para o fato de que a compatibilidade entre duas proposições está implícita na lógica clássica. Então, a partir de proposições elementares que afirmam que um sistema possui uma determinada propriedade, que pode ser avaliada testando a propriedade em uma experiência, o conceito de diálogo foi introduzido. Vários tipos de proposições compostas podem ser definidas especificando o diálogo-jogo. Ao adicionar umrelação de compatibilidade com a estrutura de Hilbert antes de construir uma lógica proposicional formal, Mittelstäedt foi capaz de completar um cálculo que é um modelo de L. Por meio desse conceito de compatibilidade, o diálogo dá um quadro completo de argumentação [185, p. 4]. Em seguida, ele introduziu modalidades e probabilidade como conceitos metalinguísticos [186, 187, 188], bem como estabelecendo que somente empregando noções adequadas de "identidade temporal" e "identidade transworld" poderia ser uma semântica de Kripke como formulada em QL [189, 190 ].

Durante os anos oitenta e noventa, em linha com a linha de pesquisa neolantina QL, o filósofo francês Michel Bitbol analisou as diferentes alternativas de linguagem das propriedades físicas e seu papel na objetividade. Embora ele admitiu que o raciocínio de Kant tinha que ser bastante alterado para se tornar aplicável ao QM, ele, no entanto, delineou uma derivação de QL de argumentos transcendentais [43]. Primeiro, a contextualidade é apontada como a principal característica que deve ser focada na aplicação do programa. No caso clássico:

[...] um fenômeno é geralmente (ou mesmo sempre) relativo a um determinado contexto que define a gama de fenômenos possíveis a que pertence. [...] Enquanto o contexto pode ser combinado, ou pelo menos enquanto os fenômenos podem ser feitos indiferentes à ordem e à cronologia do uso dos contextos, nada impede que se funda os diferentes fenômenos possíveis em relação a cada um contexto em uma única gama de possíveis conjunções de fenômenos. Ao ser feito, pode-se considerar que a nova gama de possíveis fenômenos compostos é relativa a um único e ubíquo contexto que nem sequer vale a pena mencionar. [43]

Na física clássica, as regras da lógica clássica são válidas em todos os contextos, mas também são seguras quando se fundem os contextos. Este não é o caso no QM. Embora a álgebra booleana e as leis correspondentes da lógica clássica possam ser usadas para lidar com proposições sobre qualidades em cada contexto, ao considerá-las todas juntas, a estrutura é a de L (H). Para mostrar manifestamente como as diferentes línguas se ligam, as linguagens clássicas usando conectivos clássicos são implementadas em cada contexto, então uma meta-linguagem é construída usando uma relação de implicação, ou seja, um idioma implica outro se e somente se cada sentença no primeiro é também uma frase na outra. Esta implicação é mais ampla do que a mera "união" de ambas as línguas porque contém não apenas as proposições de cada linguagem contextual, suas conjunções e disjunções, mas também novas. A combinação de contextos tem mais conseqüências do que as que ocorrem quando são usadas separadamente. Esta construção é mostrada como sendo apenas uma rede não distributiva ortográficada [42, Anexo I]. Assim, Bitbol [43] conclui que "a estrutura específica de QL é inevitável quando a unificação de linguagens contextuais a nível meta-linguístico é exigida. Nesse sentido, pode-se dizer que QL foi derivada por meio de um argumento transcendental: é uma condição de possibilidade de um meta-linguagem capaz de unificar linguagens experimentais dependentes do contexto. "Para uma revisão completa da linha neo-kantiana de pesquisa dentro da QM, nos referimos a [163]. Esta construção é mostrada como sendo apenas uma rede não distributiva ortográficada [42, Anexo I]. Assim, Bitbol [43] conclui que "a estrutura específica de QL é inevitável quando a unificação de linguagens contextuais a nível meta-linguístico é exigida. Nesse sentido, pode-se dizer que QL foi derivada por meio de um argumento transcendental: é uma condição de possibilidade de um meta-linguagem capaz de unificar linguagens experimentais dependentes do contexto. "Para uma revisão completa da linha neo-kantiana de pesquisa dentro da QM, nos referimos a [163]. Esta construção é mostrada como sendo apenas uma rede não distributiva ortográficada [42, Anexo I]. Assim, Bitbol [43] conclui que "a estrutura específica de QL é inevitável quando a unificação de linguagens contextuais a nível meta-linguístico é exigida. Nesse sentido, pode-se dizer que QL foi derivada por meio de um argumento transcendental: é uma condição de possibilidade de um meta-linguagem capaz de unificar linguagens experimentais dependentes do contexto. "Para uma revisão completa da linha neo-kantiana de pesquisa dentro da QM, nos referimos a [163].

b. Operacionalismo Lógico Quântico

O artigo de Birkhoff-von Neumann iniciou a busca de uma teoria axiomática em que a estrutura espacial de Hilbert, fisicamente não justificada, seria derivada de um conjunto de axiomas fisicamente motivados, dando particular importância ao conceito de proposições experimentais . Seguindo essa linha de pensamento, George Mackey publicou em 1963 uma monografia [179] na qual ele recuperou a idéia de von Neumann de "projeções como proposições" [234, p. 247]. Como as projeções têm apenas dois autovalores, 0 e 1, pode-se pensar na proposição associada a uma projeção como a resposta "sim" ou "não" à pergunta correspondente. Assim, Mackey referiu-se às proposições afiliadas a um sistema físico como questões[179, p. 64] e, sob uma razoável argumentação, Mackey mostrou que as questões formam uma rede ortodômica. Neste quadro, a questão de "quais medidas em questões devem ser consideradas como estados?" [179, p. 85] foi respondido pelo estudante de Mackey, Andrew Gleason:

Uma medida sobre os subespaços fechadas significa uma função μ qual atribui a cada sub espaço fechado um número real não-negativa, de tal modo que se { Um i } é uma colecção contáveis de subespaços mutuamente ortogonais tendo fechado Spam linear B , então μ ( B ) = Σ μ ( A i ). É fácil ver que essa medida pode ser obtida selecionando um vetor v e, para cada subespacial fechado A, tomando μ ( A ) como o quadrado da norma da projeção de v em A. As combinações lineares positivas de tais medidas levam a mais exemplos e, passando ao limite, descobrimos que, para cada operador auto-adjunto semi-definido positivo T da classe de traço μ ( A ) = tr ( TP A ), onde P A denota a projeção ortogonal em A , define uma medida nos subespaços fechados. O objetivo deste trabalho é mostrar que, em qualquer espaço de dimensão Hilbert separável, pelo menos três, seja real ou complexo, cada medida nos subespaços fechados é derivada dessa maneira. [144]

Em algum sentido, o programa de Mackey é uma reconstrução do QM como cálculo de probabilidade não-clássico. As investigações de Mackey sobre os fundamentos da QM renovaram o interesse no sujeito um tanto esquecido da QL, e também na sua conexão com o estudo das redes ortomodulares. Os livros de Varadarajan e Jauch [230, 159] seguem disso. Por exemplo, alguns aspectos matemáticos da noção de probabilidade envolvida pelo operador de densidade foram estudados por Veeravalli Varadarajan [229]. Mas foi o teorema de representação de Constantin Piron [194], que esclareceu o campo. O teorema afirma que, se L é uma rede atômica ortogranecida completa, que é fraca-mente modular e satisfaz a lei de cobertura, então cada componente irredutivível da rede L pode ser representado como a rede de todos os subespeitos biortogonais de um espaço vetorialV ao longo de um anel de divisão K . O teorema de Solèr prova então que um espaço ortodômico dimensional infinito sobre um anel de divisão que é o número real ou complexo ou os quaternões é um espaço de Hilbert [219].

Nos anos sessenta, Jauch e Piron [194, 159] também visavam reconstruir o formalismo do QM dos primeiros princípios com especial interesse na relação entre conceitos e operações físicas reais que podem ser realizadas no laboratório. Por exemplo, os estados são definidos como "o resultado de uma série de manipulações físicas no sistema que constituem a preparação do estado". E é enfatizado que "[t] nos estados são idênticos se as condições relevantes na preparação do estado são idênticos. (A distinção entre o sistema e seus estados não pode ser mantida em todas as circunstâncias com a precisão implícita por esta definição. O motivo é que os sistemas que consideramos diferentes em circunstâncias normais como diferentes podem ser considerados dois estados diferentes do mesmo sistema. é um positronium e um sistema de dois fótons. ) "[159, p. 92] As mesmas prescrições seguem para as proposições: "a proposição compostaa ∧ b denota a medida de a e b . "[159, Sect. 5.3] Devido à prescrição de que cada noção deve ser definida em termos de operações, esta linha de pesquisa é chamada de operacionalismo. QL operacional envolve o fato de que as respostas sim-não às perguntas elementares, ou as "proposições experimentais" de Birkhoff e von Neumann, podem ser consideradas como proposições de uma lógica não-clássica. Além disso, seu objetivo é tentar dar uma motivação independente ao programa geral para entender QM [58]. De acordo com [12], as principais linhas operacionais de pesquisa são as seguintes: a escola de Genebra comandada por Jauch e Piron [159, 195, 197] em Genebra e continuada pelo estudante de Piron, Diederik Aerts [7, 9, 10, 11 ], em Bruxelas; A aproximação de Amherst que em palavras de David Foulis e Charles Randall deve ser chamada de "lógica empírica" ​​[122, 123, 124, 127]; e, finalmente, a abordagem de Marburg dirigida por Günter Ludwig [176, 177].

Um dos principais resultados da linha operacional de pesquisa é devido a Aerts em 1981. O QL ortodoxo enfrenta um problema profundo para o tratamento de sistemas compostos. De fato, ao considerar dois sistemas clássicos, é significativo organizar todo o conjunto de proposições sobre eles na rede Booleana correspondente construída como o produto cartesiano das redes individuais. Informalmente, pode-se dizer que cada fator de rede corresponde às propriedades de cada sistema físico. Mas o caso quântico é completamente diferente. Quando dois ou mais sistemas são considerados em conjunto, o espaço de estados de seus estados puros é considerado o produto tensor de seus espaços Hilbert. Dado os espaços de Hilbert H 1 e H 2como representantes de dois sistemas, os estados puros do sistema composto são dados por raios no espaço do produto tensor H = H 1 ⊗ H 2. Mas não é verdade, como uma analogia clássica ingênua sugeriria, que qualquer estado puro do sistema composto fatorasse após a interação em estados puros dos subsistemas e que eles evoluíam com seus próprios operadores hamiltonianos. Foi mostrado, em um teorema de não separabilidade de Aerts [7], que ao tentar repetir o procedimento clássico de tirar o produto tensor das redes das propriedades de dois sistemas, obter a rede das propriedades do compósito, o procedimento falha [5, 6, 8, 57, 125, 126]. As tentativas de variar as condições que definem o produto das redes foram feitas, mas, em todos os casos, resulta que a rede de Hilbert é factorizada apenas no caso em que um dos fatores é uma rede booleana ou quando os sistemas nunca interagiram. Usando a abordagem operacionista dois estudantes belgas de Aerts, Bob Coecke e Sonja Smets, delinearam um programa de pesquisa sobre QL dinâmico. [62, 60, 218] (ver Seção 5.2).

c. Quantum Logic é empírico?

No final dos anos sessenta e no início dos anos setenta, havia uma visão filosófica radical iniciada por David Finkelstein [120, 121] e Hilary Putnam [202, 203] argumentando que a lógica é, em certo sentido, empírica.

Finkelstein destacou as abstrações que fazemos passando da mecânica para a geometria para a lógica e sugerimos que os processos dinâmicos de fratura e fluxo já observados nos dois primeiros níveis também deveriam surgir no terceiro. Putnam, por outro lado, argumentou que as patologias metafísicas de superposição e complementaridade não são mais que artefatos de contradições lógicas geradas por um uso indiscriminado da lei distributiva. [58]

De acordo com o famoso artigo de Putnam [202]: "A lógica é tão empírica como a geometria. Vivemos em um mundo com uma lógica não clássica. "Para Putnam nesse período específico, os elementos de L (H) representam propriedades categóricas que um objeto possui ou não possui, independentemente de olhar ou não. Na medida em que esta imagem de propriedades físicas é confirmada pelo sucesso empírico de QM, essa visão significa que devemos aceitar que a maneira pela qual as propriedades físicas realmente se encaixam não é booleana. Como a lógica é, para Putnam, muito o estudo de como as propriedades físicas realmente se mantêm unidas, ele conclui que a lógica clássica é simplesmente enganada: a lei distributiva não é universalmente válida.

d. Interpretações Modais

O estudo do caráter modal da QM foi explicitamente formalizado nos anos setenta e oitenta por um grupo de físicos e filósofos da ciência. Bas van Fraassen foi o primeiro a incluir formalmente o raciocínio da lógica modal no QM. Ele apresentou uma interpretação modal (MI) da QL em termos de análise semântica [224, 225, 226, 227]. O objetivo era clarificar quais propriedades entre as do conjunto completo estruturado na rede de subespaços do espaço de Hilbert pertencem ao sistema. A posição de Van Fraassen permanece próxima da tradição introduzida por Niels Bohr e sua interpretação da QM. De fato, a relação da interpretação de Van Fraassen com a visão ortodoxa pode ser vista como uma conseqüência de manter uma posição "conservadora" em relação aos valores de propriedades definidas [228, p. 280].

Em 1985, Simon Kochen apresentou sua própria versão modal [166] em uma das famosas conferências sobre os fundamentos da QM organizados por Kalervo Laurikainen na Finlândia. Esta interpretação da QM também tem um link direto para as discussões entre os fundadores da teoria. Von Weizsäcker e Thomas Görnitz referiram-se especificamente a ele em um artigo intitulado "Observações sobre a Interpretação de Mecânica Quântica de S. Kochen":

Consideramos que é um aclarante esclarecimento da estrutura matemática da teoria, especialmente para descrever o processo de medição. Nós, no entanto, sentimos que isso não significa uma alternativa, mas uma continuação da interpretação de Copenhague (Bohr e, até certo ponto, Heisenberg). [236, p. 357]

A interpretação de Dennis Dieks pode ser considerada como uma continuação e um relato formal das idéias de Bohr sobre complementaridade e medição. Tomando como ponto de vista o trabalho feito por van Fraassen, Dieks foi mais longe em relação aos pressupostos metafísicos envolvidos, explicando a idéia de que os MIs [94, 95, 96, 97] também poderiam ser considerados de uma postura realista como descrevendo sistemas com propriedades . Se considerarmos dessa perspectiva, os IM enfrentam o problema de encontrar uma leitura objetiva do formalismo matemático aceito da teoria, uma leitura "em termos de propriedades possuídas pelos sistemas físicos, independentemente da consciência e das medidas (no sentido das intervenções humanas). "[97] Assim, o principal problema que devem enfrentar é a determinação do conjunto de propriedades definidas valorizadas por um sistema físico, evitando as restrições impostas pelo teorema de Kochen-Specker (KS) [167] (para uma discussão, consulte [220]). Claro, a forma como os MIs atacam o problema recai sobre a distinção entre os domínios depossibilidade e realidade .

Como observado por Dirac no primeiro capítulo de seu famoso livro [99], a existência de superposições é responsável pela diferença marcante entre comportamento quântico e clássico. As superposições também são fundamentais quando se trata do processo de medição, onde os vários termos associados aos possíveis resultados de uma medida devem ser considerados presentes na descrição. Este fato leva van Fraassen à distinção entre proposições-atribuir valor e proposições-atribuindo estaduais , entre valor-estados e dinâmicas-estados :

[...] um estado , que está no escopo da mecânica quântica, nos dá apenas probabilidades de ocorrência real de eventos que estão fora desse escopo. Eles não podem estar totalmente fora do escopo, uma vez que os eventos são certamente descritos se forem atribuídos probabilidades; mas pelo menos não são as mesmas coisas que os estados que atribuem a probabilidade.

Em outras palavras, o estado delimita o que pode e não pode ocorrer, e o quão provável é: delimita a possibilidade, a impossibilidade e a probabilidade de ocorrência, mas não diz o que realmente ocorre. [228, p. 279]

Assim, van Fraassen distingue proposições sobre eventos e proposições sobre estados. Proposições sobre eventos são proposições de atribuição de valor <A, σ> , dizem que " A observável tem um certo valor pertencente a um conjunto σ. "As proposições sobre estados são da forma" o sistema está em um estado desse ou aquele tipo (em um estado puro, em alguma mistura de estados puros, em um estado tal que ...) ". Uma proposição de atribuição de estado [ A, σ ] dá uma probabilidade da proposição de atribuição de valor, afirma que A terá um valor em σ , com certa probabilidade. Estado de valoressão especificados afirmando quais valores observáveis ​​têm valores e quais são esses valores. Os estados dinâmicos indicam como o sistema irá desenvolver. Isto é dotado da seguinte interpretação:

A interpretação diz que, se um sistema X tiver um estado dinâmico ρ em t , as atribuições de estado [ A, σ ] que são verdadeiras são as que Tr ( ρP σ A ) = 1 [têm probabilidade igual a uma]. [ P σ A  é o projetor sobre o subespaço correspondente.] Sobre as atribuições de valor, diz que elas não podem ser deduzidas do estado dinâmico, mas são restritas de três maneiras:

1. Se [ A, σ ] for verdadeiro, então a atribuição de valor <A, σ> : A observável tem valor em σ .
2. Todas as atribuições de valor verdadeiro devem ter a probabilidade 1 de nascimento juntas.
3. O conjunto de atribuições de valor verdadeiro é máximo em relação ao recurso (2.) [228, p. 281]

Esta interpretação informa a consideração de possibilidade no âmbito da QL [228, capítulo 9]. Na verdade, as probabilidades são de eventos, cada um descrito como "um observável com um certo valor", correspondente a estados de valor. Se w é uma situação física em que o sistema X existe, então X possui um estado dinâmico φ e um estado de valor λ , isto é, w = <φ, λ> . Um estado valor λ é um mapa de observável A em não-vazia Borel define σ tal que atribui {1} para 1 σ A . 1 σé a função característica do conjunto σ de valores. Então, se o 1 σ A observável tiver o valor 1, é impossível que A tenha um valor fora de σ . A proposição <A, σ> = { w : λ ( w ) ( A ) ⊆ σ } atribui valores a magnitudes físicas. Esta é uma proposição de atribuição de valor e é lida como ' A (na verdade) tem valor em σ '. V é chamado de conjunto de atribuições de valor V = { <A, σ> : A a observável e σum conjunto de Borel}. As operações de lógica entre proposições de atribuição de valor são definidas como:

<A, σ> ⊥ = <A, 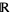 - σ> , <A, σ> ∧ <A, θ> = <A, σ ∩ θ> , <A, σ> ∨ <A, θ> = <A, σ ∪ θ> e ∧ { <A, σ i > : i ∈ N} = <A, ∩ { σ i : i ∈ N} > .

Com tudo isto, V é a união de uma família de sigma álgebra booleana <A> com unidade comum e de zero igual a <A, S ( O ) > e <A, ∧ > respectivamente. A Lei do Médio Excluído está satisfeita: cada situação w pertence a q ∨ q ⊥ , mas não a Lei da Bivalência: a situação w não pode ser nem qnem q ⊥ .

Um estado dinâmico φ é uma função de V em [0, 1], cuja restrição para cada sigma álgebra booleana <A> é uma medida de probabilidade. A relação entre estados dinâmicos e valores é a seguinte: φ e λ são um estado dinâmico e um estado de valor, respectivamente, apenas se houver situações possíveis w e w 'tal que φ = φ ( w ) , λ = λ ( w' ) . Aqui, φ é um eigenstate de A , com o autovalor correspondente a , exatamente se φ (<A, { a } > ) = 1. A proposição de atribuição de estado [ A, σ ] é definida como: [ A, σ ] = { w : φ ( w ) ( <A, σ> ) = 1} e significa ' A deve ter valor em σ '. P  indica o conjunto de proposições de atribuição de estado: P = {[ A, σ ]: A um observável , σum conjunto de Borel}. A ordem parcial entre eles é dada por [ A, σ ] ⊆ [ A ', σ'  ] somente se, para todos os estados dinâmicos φ ,φ ( <A, σ> ) ≤ φ ( <A ' σ ' > ) e as operações lógicas são (bem) definida como: [ A, σ ] ⊥ = [ A, 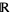 - σ ], [ A, σ ] ⊎$<span\; style="border:\; 0px;\; font-style:\; inherit;\; font-weight:\; inherit;\; margin:\; 0px;\; outline:\; 0px;\; padding:\; 0px;\; transition:\; none;\; vertical-align:\; inherit;"><span\; style="border:\; 0px;\; font-style:\; inherit;\; font-weight:\; inherit;\; margin:\; 0px;\; outline:\; 0px;\; padding:\; 0px;\; transition:\; none;\; vertical-align:\; inherit;">\uplus </span></span>$[ A, θ ] = [ A, σ ∪ θ ] e [ A, σ ] ∩ [ A, θ ] = [ A, σ ∩ θ]. Com tudo isso, <P, ⊆ , ⊥ > é um orthoposet. O orthoposet é formado por "colar" uma família de álgebras booleanas em que operações inteiras coincidem em áreas sobrepostas. Pode ser enriquecido para se aproximar da rede de subespaços do espaço de Hilbert.

Pode-se reconhecer uma relação modal entre ambos os tipos de proposições. Por exemplo, começa-se a negar o colapso no processo de medição e reconhecendo que o observável possui um dos autovalores possíveis. Então, pode ser perguntado o que pode ser inferido em relação a esses valores quando se conhece o estado dinâmico. A resposta Van Fraassen dá é que, no caso de φ ( w ) é um eigenstate do A observável com autovalor a , então A realmente tem valor a . Isso significa que, neste caso, a medição "revela" o valor que o observável já teve. Ele generaliza essa idéia e postula que [ A, σ ] implica <A, σ>. Com essa suposição e a rejeição de uma interpretação de ignorância do princípio da incerteza, ele é capaz de provar que [ A, σ ] = □ <A, σ> . O operador de necessidade □ é definido por □ Q = { w : para todos w ', se wRw ' então w '∈ Q }, onde Q é qualquer proposição e R é a relação de possibilidade relativa: w ' é possivelmente relativo a w exatamente se , para todos Q em V, se w estiver em Q então w'Está em Q . Assim, [ A, σ ] pode ser lido como 'necessariamente, <A, σ> '. Isso diz que o estado dinâmico atribui 1 a <A, σ> se e somente se o estado do valor que acompanha qualquer estado dinâmico relativamente possivel faz com que <A, σ> seja verdade. Em vez da relação de possibilidade transitiva R , pode-se usar uma relação de equivalência para definir □ ',  o operador de necessidade negada. Neste caso, van Fraassen sustenta que o mapa [ A, σ ] → <A, σ> é um isomorfismo de posets <P, ⊆ > e <V, ⊆ >e, quando a ortoplasma é definida, torna-se um isomorfismo entre os ortopostos. Assim, a lógica de V é a de P , isto é, QL. Dotado dessas ferramentas, van Fraassen dá uma interpretação das probabilidades dos resultados da medida que está de acordo com a regra de nascimento.

O MI proposto por Kochen e Dieks (KD, para abreviar), propõe usar o chamado teorema de decomposição biortogonal (também chamado de teorema de Schmidt) para descrever as correlações entre o sistema quântico e o aparelho no processo de medição. De uma perspectiva realista, uma questão de interpretação que os MIs precisam levar em consideração é a atribuição de valores definitivos às propriedades. Mas se tentarmos interpretar os valores próprios que pertencem a diferentes conjuntos de observáveis ​​como valores reais (pré-existentes) das propriedades físicas de um sistema, enfrentamos todos os tipos de teoremas de não-retorno que impedem essa possibilidade. Quanto ao esquema específico do MI, Bacciagaluppi e Clifton conseguiram derivar as contradições do tipo KS na interpretação do KD, que mostrou que não se pode estender o conjunto de propriedades definidas para sub-sistemas não disjuntos [26, 56]. Para escapar das contradições do tipo KS, a versão modal de Jeffrey Bub lembra a interpretação de David Bohm e propõe-se a levar alguns observáveis,R , como sempre possuindo um valor definido. Desta forma, pode-se evitar as contradições KS e manter um discurso consistente sobre declarações que pertencem ao sublattice determinado pelo R observável preferido . Tal como acontece com as interpretações de Van Fraassen e Vermaas e Dieks, a proposta de Bub distingue entre estados dinâmicos e estados de propriedade ou valor, no seu caso com o objetivo de interpretar a função de onda como definindo uma medida de probabilidade Kolmogoroviana em uma sub-algebra restrita da rede L (H) das operações de projeção (correspondentes a experiências sim-no) sobre o espaço de estados. É essa distinção entre estados de propriedade e estados dinâmicos que, de acordo com Bub, fornece o caráter modal à interpretação:

A idéia por trás de uma interpretação "modal" da mecânica quântica é que os estados quânticos, ao contrário dos estados clássicos, restringem as possibilidades ao invés de atualizações - o que deixa a questão de se pode introduzir estados de propriedade [...] que atribuem valores a (alguns) observáveis ​​da teoria, ou equivalentemente, valores de verdade para as proposições correspondentes. [47, p. 173]

Em termos precisos, como L (H) não admite uma família global de avaliações compatíveis e, portanto, nem todas as proposições sobre o sistema são determinadamente verdadeiras ou falsas, as probabilidades definidas pelo estado (puro) não podem ser interpretadas epistemicamente [47] (p . 119). Mas, se alguém escolhe, para um determinado estado | e>, um R observável preferido, essas propriedades podem ser consideradas como determinadas, uma vez que as proposições associadas a R, isto é, com os projetores em que R se decompõe, geram uma álgebra booleana. Bub constrói os sublatórios máximos
D (| e>, R) ⊆ L (H) para o qual os valores de verdade podem ser atribuídos através de um homomorfismo de 2 valores e demonstração de teorema de singularidade que permite uma construção do observável preferido.

Na proposta de Bub, um estado de propriedade é uma especificação máxima das propriedades do sistema em um momento específico, definido por um homomorfismo booleano a partir da sublattice determinada para a álgebra booleana de dois elementos. Por outro lado, um estado dinâmico é um átomo de L (H) que evolui unitariamente no tempo, seguindo a equação de Schrödinger. Assim, estados dinâmicos não coincidem com estados de propriedade. Dado um estado dinâmico representado pelo átomo | e>  ∈ L ( H ), um constrói o sublattice D (| e> , R) com probabilidades de Kolmogorovian definidas sobre subconjuntos alternativos de propriedades no sublattice. São as propriedades do sistema e as probabilidades definidas por | e>  evoluir (através da evolução de | e> ) no tempo. Se o observável preferido é o operador de identidade I , os átomos em D (| e> , I ) podem ser retratados como um "ventilador" de seus projetores gerados pelo "identificador" | e>  [46, p. 751] ou um "guarda-chuva" com estado | e>  novamente como o identificador e os raios em (| e> ) ⊥ como espinhos. Quando observável R ≠ I , existe um conjunto de alças {| e ri>, i = 1 ... k } dado pelas projeções diferentes de zero de | e>  para os espaços iguais de R e as espinhas representadas por todos os raios no complemento ortogonal do subespaço gerado pelas alças. Quando fraca ( H ) > 2, existem k homomorphisms 2-valiosos que mapeiam cada uma das alças para 1 e os átomos restantes no 0. A subrede determinado, que muda com a dinâmica do sistema, é uma álgebra booleana parcial, que é a união de uma família de álgebras booleanas coladas de forma a que os elementos máximo e mínimo de cada um e eventualmente outros elementos sejam identificados e, para cada n- múltiplos elementos compatíveis com pares, existe uma álgebra booleana na família que contém os n elementos. A possibilidade de construir um espaço de probabilidade em relação ao qual as probabilidades de Born geradas por | e>  pode ser pensado como medidas sobre subconjuntos de estados de propriedade, depende da existência de muitos estados de propriedade suficientes como homomorfismos de 2 valores sobre D (| e> , R). Isto é garantido por um teorema de singularidade que caracteriza D (| e> , R ) [47, p. 126]. Assim construído, a estrutura evita os teoremas do tipo KS. Em seguida, dado um sistema S e um aparelho de medição M ,

[...] se alguma quantidade R de M é designada como sempre determinada e M interage com Satravés de uma interação que estabelece uma correlação entre os valores de R e os valores de alguma quantidade A de S , então A torna-se determinado em a interação. Além disso, o estado quântico pode ser interpretado como atribuição de probabilidades às diferentes maneiras possíveis pelas quais o conjunto de quantidades determinadas pode ter valores, onde um determinado conjunto de valores representa os valores reais mas desconhecidos dessas quantidades . [46, p. 750]

O problema com esta interpretação é que, no caso de um sistema isolado, não há um único elemento no formalismo do QM que nos permita escolher um R observável , e não outro. É por isso que o movimento parece flagrantemente ad hoc . Se estivéssemos lidando com um aparelho, haveria uma observação preferida, ou seja, a posição do ponteiro, mas a função da onda quântica contém em si mesmas representações mutuamente incompatíveis (opções de aparelhos), cada uma das quais fornece informações não triviais sobre o estado de coisas. A proposta Bohmian de Bub, foi ampliada por Guido Bacciagaluppi e Michael Dickson em sua versão atômica do MI [27].

Os autores deste trabalho também contribuíram para a compreensão da modalidade no contexto da QL ortodoxa [102, 103, 104, 105]. Da nossa investigação, existem várias conclusões que podem ser desenhadas. Começamos nossa análise com uma pergunta sobre o aspecto contextual da possibilidade. Como é bem sabido, o teorema do KS não fala sobre probabilidades, mas sim sobre as restrições do formalismo para propriedades reais definidas, consideradas em múltiplos contextos. O que encontramos através da análise de possíveis famílias de avaliações é o teorema que chamamos, por razões óbvias, o teorema do KS Modal (MKS) pode ser derivado, o que prova que a possibilidade quântica, ao contrário da possibilidade clássica, também é contextualizada [102 ]. Isso significa que, independentemente da sua utilização na literatura,A possibilidade quânticanão é uma possibilidade clássica . Em um artigo escrito em 2014 [88], nos concentramos na análise da atualização dentro do quadro ortodoxo e interpretamos, seguindo a estrutura, o domínio lógico da possibilidade em termos de potencialidade ontológica.

e. As escolas checo-eslovaca e italiana

O estudo da estrutura dos produtos tensores [57, 199, 112, 113, 114] motivou um desenvolvimento frutífero de diferentes estruturas algébricas que poderiam representar proposições quânticas, que por sua vez se tornaram uma linha de investigação por si só. Começando com a proposta de espaços de teste por Foulis e Randall [122, 123, 124, 204, 206, 207], que estão relacionados às ortoalgebras, a teoria das estruturas como redes ortomodulares, álgebras booleanas parciais, posets ortomodulares, álgebras de efeito , as álgebras MV quânticas e similares tornaram-se amplamente discutidas. A escola checa liderada por Pavel Ptak, a escola eslovaca iniciada por Anatolij Dvurečenskij e Sylvia Pulmannová e a escola italiana organizada por Enrico Beltrametti e Maria Luisa Dalla Chiara e continuada por Roberto Giuntini foram pioneiras no assunto, veja, por exemplo [32, 33, 36, 37, 52, 51, 54, 78, 79, 81, 115, 113, 130, 128, 129, 145, 141, 142, 148, 147, 168, 162, 169, 198, 200, 237, 238]. As estruturas enfraquecidas permitem a consideração de proposições unsharp relacionadas, não a projeções, mas aos elementos do conjunto mais geral de operadores limitados lineares - chamadosefeitos sobre os quais a medida de probabilidade dada pela regra de nascimento pode ser definida. E isso, por sua vez, deu origem à consideração de QL paraconsistente, QL parcial e Łukasiewickz QL [79].

Uma importante linha de pesquisa sobre o assunto de estruturas quânticas é a aplicação de métodos QL a linguagens de processamento de informação e, mais especificamente, à lógica computacional quântica (QCL) [53, 80, 101, 82, 135, 136, 138, 143 , 149, 193, 192]. Desta forma, foram desenvolvidos vários sistemas lógicos associados à computação quântica. Eles fornecem uma nova forma de lógica quântica fortemente conectada com a lógica difusa de t -norms contínuos [151]. Os grupos de Firenze, dirigidos por Dalla Chiara e Cagliari, dirigidos por Giuntini, também desenvolveram diferentes linguagens para a computação quântica. Uma frase em QL pode ser interpretada como um subespaço fechado de H. Em vez disso, o significado de uma sentença elementar em QCL é uma quantidade de informação quântica codificada em uma coleção de qbits- vetores unitários pertencentes ao produto tensorial de espaços de Hilbert complexos bidimensionais - ou qmixes - operadores semi-definidos de hermitios posicionais de um traçado um sobre o espaço de Hilbert. Conjunção e disjunção não estão associadas à junção e às operações de rede. Em vez disso, o número de conjunções e disjunções envolvidas em uma sentença determina a dimensão do espaço de seus "significados", a dimensão variando com o número e natureza dos conectivos lógicos, assim o "significado" da frase reflete a forma lógica de a própria frase (para uma discussão completa, veja [80]).

f. A Escola Brasileira

Newton da Costa e Décio Krause em Florianópolis iniciaram investigações sobre Lógica não Reflexiva (LNR) e Lógica Paraconsistente (PL) relacionadas a várias questões fundamentais em relação à QM. Por um lado, NRL é, em um sentido amplo, uma lógica na qual a relação de identidade (ou igualdade) é restrita, eliminada, substituída, pelo menos em parte, por uma relação mais fraca ou empregada em conjunto com uma nova não- implicação reflexiva ou relação de equivalência. Na lógica clássica, um dos princípios básicos é o Princípio da Identidade (PI), expressando a propriedade reflexiva da identidade, cuja formulação usual é x = x ou ∀ x ( x = x ), onde xé uma variável de primeira ordem. Existem outras versões em lógica de ordem superior, nas quais variáveis ​​de ordem superior aparecem. Existem também formulações proposicionais do princípio: p → p ( p implica p ) ou p ↔ p ( p é equivalente a p ), onde p é uma variável proposicional. Se a quantificação proposicional é permitida, temos outras formas do princípio: ∀ p( p → p ), bem como: ∀ p ( p ↔ p). Alguns dos princípios acima não são, em geral, válidos em lógicas não reflexivas. Eles são total ou parcialmente eliminados, restritos ou não aplicados na relação que é empregada em vez de identidade. Vários desses princípios são as motivações para o desenvolvimento de lógicas não reflexivas. A aplicação do PI é controversa no domínio quântico, não só devido à chamada "indistinguibilidade das partículas quânticas", mas, mais profundamente, ao aplicá-la a "algo" que não respeita a definição clássica de objeto. Em particular, a busca por uma teoria de conjuntos que poderia ser adequada à QM é tão antiga quanto o Congresso da Sociedade Matemática Americana de 1974, dedicado à avaliação do status dos problemas de Hilbert no século, colocado em Paris em 1900 No Congresso de 1974,

[...] devemos considerar as possibilidades de desenvolver uma linguagem totalmente nova para falar sobre o infinito. [...] Gostaria de salientar que este [o conceito de conjunto] é mais uma extrapolação da física do lugar comum, onde podemos distinguir as coisas, contá-las, colocá-las em ordem, etc. Nova física quântica mostrou modelos de entidades com comportamento bastante diferente. Mesmo "conjuntos" de fótons em uma caixa de espelho, ou os elétrons em uma peça de níquel são muito menos cantorianos que o "conjunto" de grãos de areia. [181]

O "novo idioma para falar sobre o infinito" é, obviamente, uma nova teoria "set", uma vez que a teoria dos setores é geralmente conhecida como "a teoria do infinito (real)". Para uma discussão sobre a necessidade de uma nova teoria de conjuntos, veja por exemplo [171, 134, 170, 77]. Nesse contexto, o enfraquecimento do conceito de identidade - substituído pelo de indiscernibilidade - permite o desenvolvimento de lógicas não reflexivas que, em um sentido amplo, são lógicas nas quais a relação de identidade (ou igualdade) é restrita, eliminada, substituído, pelo menos em parte, por uma relação mais fraca, ou empregado em conjunto com uma nova relação de implicação ou equivalência não reflexiva [68, 73, 172, 75]. Existem também abordagens diferentes da lógica relacionada às teorias de conjuntos quânticos. Gaisi Takeuti propôs uma teoria de conjuntos quânticos desenvolvida na rede de universo estimado de projeções [221,

Por outro lado, PL são as lógicas de teorias inconsistentes, mas não triviais. As origens de PL retornam aos primeiros estudos sistemáticos que tratam da possibilidade de rejeitar a PNC. PL foi elaborado, de forma independente, por Stanislaw Jaskowski na Polônia e por Newton da Costa no Brasil, em meados do século passado (em PL, veja, por exemplo: [72]). Uma teoria T fundada na lógica L , que contém um símbolo de negação, é chamada de inconsistente se tiver entre seus teoremas uma sentença A e sua negação ¬ A ; Caso contrário, é dito ser consistente. T é chamado de trivial se qualquer frase de sua linguagem for também um teorema de T ; caso contrário, Té dito não trivial. Nas lógicas clássicas e nas lógicas mais usuais, uma teoria é inconsistente se, e somente se, é trivial. eué paraconsistente quando pode ser a lógica subjacente de teorias inconsistentes, mas não triviais. Claramente, nenhuma lógica clássica é paraconsistente. No contexto da QM, da Costa e Krause apresentaram [71] um PL para fornecer um esquema formal adequado para considerar a noção de complementaridade introduzida em 1927 por Niels Bohr durante sua famosa "Palestra de Como". A noção de complementaridade foi desenvolvida por Bohr para considerar as representações contraditórias da representação das ondas e da representação corpuscular encontrada no experimento de dupla fenda (ver, por exemplo, [174]). De acordo com Bohr: "Devemos, em geral, estar preparado para aceitar o fato de que uma elucidação completa de um mesmo objeto pode exigir diversos pontos de vista que desafiam uma descrição única.

5. Desenvolvimentos em andamento e debates

Há uma grande quantidade de trabalho em progresso na QL de novas estruturas quânticas, ao uso de lógicas não reflexivas, lógicas paraconsidentes, lógicas dinâmicas, etc. Na seção a seguir, analisaremos alguns desses avanços que ocorreram em relação para QM.

a. Novas Estruturas Quânticas

A importância das estruturas quânticas como campo de pesquisa deu origem a sua própria associação: a International Quantum Structures Association (IQSA) . Como diz Dvurečenskij no Prefácio ao Manual de Lógica Quântica e Estruturas Quânticas :

[...] no início dos anos 90, uma nova organização chamada International Quantum Structures Association (IQSA) foi fundada. IQSA reúne especialistas em lógica quântica e estruturas quânticas de todo o mundo sob seu guarda-chuva. Organismos de reuniões bianuais regulares: Castiglioncello 1992, Praga 1994, Berlim 1996, Liptovsky Mikulas 1998, Cesenatico 2001, Viena 2002, Denver 2004, Malta 2006. Na primavera de 2005, Dov Gabbay, Kurt Engesser, Daniel Lehmann e Jane Spurr tiveram uma excelente ideia - pedir a especialistas em lógica quântica e estruturas quânticas para escrever longos capítulos para o Manual de Lógica Quântica e Estruturas Quânticas. [117, p. viii]

De fato, no sujeito de estruturas quânticas, as álgebras MV, álgebras de efeitos, álgebras de pseudo-efeito e estruturas relacionadas estão sendo desenvolvidas em relação ao seu uso em QM. Veja [55, 116, 131, 132, 133, 184, 201], apenas para citar alguns exemplos.

b. Lógica dinâmica, Teoria da categoria e Computação Quântica

Conforme mencionado acima (ver Seção 4.2), Smets e Coecke iniciaram uma linha de pesquisa que considera a possibilidade de considerar QL de forma dinâmica. Esta pesquisa está ligada à tradição da ciência da computação, interessada na noção semântica de processo e pensa sobre o reino quântico em termos de mudança, em vez de tomar conceitos como "partícula", "sistema", "propriedade" e assim por diante como fundamental. O ponto de vista desta abordagem é a observação de que QL é essencialmente uma lógica dinâmica, que se trata de açõesem vez de proposições [30]. Também está relacionado com a interpretação do "Sasaki hook" - ou seja, a implicação quântica mais próxima da clássica - que pode ser entendida em termos de uma modalidade dinâmica em vez de em termos de dedução - de fato, ela faz não satisfaça o teorema da dedução [60]. Smast juntamente com Alexandru Baltag propuseram duas axiomatizações da lógica das ações quânticas [218]. Um deles leva a noção de ação como fundamental e axioma a álgebra subjacente, dando uma quantia [22, 59]. O outro leva a noção de estado como fundamental e representa ações como relações entre estados. Ao contrário da QL ortodômica [78], essas axiomatizações cumprem a plenitude em relação aos espaços infinitos de Hilbert dimensional e têm aplicações em ciência computacional [28]. De fato, a aplicação à ciência computacional e, mais amplamente, ao processamento da informação precisa gerenciar sistemas compostos, uma das dificuldades profundas que enfrenta QL ortodoxa.

Além disso, a relação entre a teoria das categorias e QL está sendo explorada a partir de diferentes perspectivas. De um lado, há uma linha de investigação iniciada por Chris Isham e continuada por Andreas Döring com Chris Heunen, Klaas Landsman e Bas Spitters entre outros, cujo principal interesse é ligar a construção de uma teoria física e sua representação em um topos [146] do idioma formal unido à teoria [107, 108, 109, 110, 157, 111, 154, 50]. Eles fazem afirmações sobre a necessidade de rever os supostos básicos que são obtidos, como, por exemplo, a natureza do espaço-tempo, o uso de números reais como valores de quantidades físicas e o significado de probabilidade. Do ponto de vista lógico, ao contrário da QL intratável, qualquer topos em que a teoria física é representada vem com uma lógica intuicionista intrínseca que, obviamente, é mais tratável. Além disso, os sistemas compostos também encontram seu lugar na abordagem topos [111]. As teorias clássicas estão incluídas nesta nova formalização e, para todas elas, o correspondente topos é o de conjuntos dotados de lógica clássica como intuitivo trivial. Também Elias Zafiris e Vassilios Karakostas estão fazendo novas pesquisas em semântica categorial [239].

Por outro lado, a linha de investigação iniciada em Oxford por Samson Abramsky e continuada por Coecke entre outros propôs uma axiomatização que pode ser útil para gerenciar a linguagem formal de processos físicos envolvidos em novas tecnologias quânticas como computação quântica e teletransporte. Os computadores quânticos exploram a existência de superposições para diminuir drasticamente o tempo e os recursos necessários para lidar com determinados problemas, como a descoberta triangular, a factorização inteira ou a busca de uma entrada em uma lista desordenada [164, 191]. A teletransporte usa a não separabilidade para transmitir informações de forma segura de um lugar para outro por meio de um estado emaranhado e um canal de comunicação clássico [45]. A abordagem categórica do grupo de Oxford usa categorias monoidais [1, 2, 3, 4, 67, 165] e diagramas simples para visualizar processos quânticos e sistemas compostos de forma consistente. Eles aplicam essas ferramentas para pesquisar no assunto da semântica de computação [63, 64, 65], em particular no assunto da lógica linear [140], que é essencial para a ciência da computação. Também Cristina e Amilcar Sernadas em Lisboa estão trabalhando na conexão da teoria das categorias e da lógica linear [182, 183, 49].

Pesquisas sobre semântica computacional estão sendo desenvolvidas em conexão com lógicas epistêmicas por membros do grupo italiano. Por exemplo, eles modelam operadores como "entender" ou "conhecer" por operações quânticas irreversíveis, permitindo assim refletir sobre limitações características no processo de aquisição de informações [34, 35]. A relação entre estruturas quânticas e lógicas epistêmicas também está sendo estudada por um grupo em Amsterdã. Eles estão aplicando uma QL dinâmica-epistêmica modal para o raciocínio sobre os algoritmos quânticos e, em geral, para considerar os sistemas quânticos como ações codificantes de produção e processamento de informações [29, 30, 31].

A dinâmica dos conceitos estudados pela ciência cognitiva também está sendo considerada com a ajuda de estruturas quânticas. De fato, D. Aerts e colegas de trabalho aplicaram o formalismo da QM para modelar a combinação de conceitos, mostrando os caracteres indeterministas e holísticos desse processo [13, 16, 17, 20, 21]. Esta abordagem tem aplicações tecnológicas em conexão com computação quântica e robótica [18, 19].

c. Parasão e superposições quânticas

Como observado por Coecke, o significado do princípio da superposição pode ser a chave para entender QM:

Birkhoff e von Neumann criaram lógica quântica para enfatizar a noção de superposição quântica. Em termos de estados de um sistema físico e propriedades desse sistema, a superposição significa que a propriedade mais forte que é verdadeira para dois estados distintos também é verdadeira para estados diferentes dos dois. Nos termos teóricos da ordem, isto significa, representando estados pelos átomos de uma rede de propriedades, que a união p∨ q de dois átomos p e q também está acima de outros átomos. A partir disso, segue facilmente que a lei distributiva quebra: dado átomo r  ≠ p, q com r <p ∨ q temos r ∧ ( p∨ q ) = r enquanto ( r ∧ p ) ∨ ( r ∧ q ) = 0∨0 = 0. Birkhoff e von Neumann, bem como muitos outros acreditavam que entender a estrutura profunda da superposição é a chave para obter uma melhor compreensão de teoria quântica como um todo. [66]

De acordo com essa intuição, em [74], um dos autores deste artigo junto com N. da Costa argumentou em favor da possibilidade de considerar superposições quânticas em termos de abordagem PL. Alegou-se que, apesar de a maioria das interpretações da QM tentar escapar das contradições, há muitas sugestões - provenientes principalmente dos atuais desenvolvimentos técnicos e experimentais da QM - que indicam que poderia valer a pena se envolver em uma pesquisa desse tipo. Arenhart e Krause [23, 24, 25] levantaram vários argumentos contra a abordagem paraconsistente às superposições quânticas que foram analisadas posteriormente em [86]. Recentemente, algumas novas propostas para considerar superposições quânticas de uma perspectiva lógica foram apresentadas [76, 173].

d. Contradição e Modalidade no Quadrado da Oposição

Na lógica clássica aristotélica, as proposições categóricas são divididas em afirmações universais afirmativas, negativas universais, afirmações particulares e negativas particulares. As possíveis relações entre dois tipos de proposições mencionadas são codificadas no quadrado de oposição. O quadrado expressa as propriedades essenciais da quantificação monadica de primeira ordem que, em uma abordagem algébrica, pode ser representada levando em consideração álgebras booleanas monadicas. O quadrado de oposição foi considerado, em relação à QL, como uma ferramenta útil para identificar negações paraconsistentes [38, 40]. O quadrado também expressa as propriedades essenciais dos quantificadores monádicos de primeira ordem ∃ e ∀ que, em uma abordagem algebraica, podem ser representados dentro do quadro de álgebras booleanas monadicas, considerando os quantificadores como operadores modal atuando em uma álgebra booleana [150]. Essa representação é chamada de quadrado modal de oposição. Uma extensão do quadrado para um caso em que a estrutura subjacente é substituída pela álgebra de QL foi fornecida em [137] e pode ser útil identificar negações paraconsistentes na estrutura de QM (veja também para discussão [89]) .

O quadrado de oposição também foi recentemente considerado em relação ao significado das superposições quânticas e à interpretação dos termos que a compõem (Seção 5.3). Por um lado, de acordo com [74], argumentou-se que se poderia considerar alguns dos termos que compõem a superposição como contraditórios . Por outro lado, Arenhart e Krause [23, 24, 25] defenderam a ideia de que, levando em consideração o quadrado da oposição, a contrariância é uma noção mais adequada para descrever o significado físico das superposições (ver também [85, 86, 87]).

e. Probabilidade quântica

O assunto da probabilidade no QM aparece nas primeiras discussões e análises fornecidas pelos fundadores da teoria. Por um lado, há a questão da sua interpretação, já sublinhada por Schrödinger em uma carta a Einstein: "Parece-me que o conceito de probabilidade é terrivelmente maltratado hoje em dia. A probabilidade certamente tem como substância uma declaração sobre se algo é ou não o caso - de uma declaração incerta, com certeza. Mas, no entanto, só tem sentido se alguém estiver realmente convencido de que o algo em questão é definitivamente o que não é o caso. Uma afirmação probabilística pressupõe a plena realidade de seu assunto ". [47, p. 115]. Por outro lado, um enfrenta o problema de sua própria definição: A regra de Born foi incorporada na axiomatização da QM como uma medida não-comutativa sobre a rede de eventos de von Neumann no início dos anos trinta, mas essa medida precisa de uma rede modular para ser bem posicionada, enquanto L (H) é ortomodular. Como Miklos Rédei afirma:

Para ver por que von Neumann insistiu na modularidade da lógica quântica, é preciso entender que ele queria que a lógica quântica não fosse apenas o cálculo proposicional de um sistema mecânico quântico, mas também queria que ele servisse como a estrutura do evento no sentido da teoria da probabilidade . Em outras palavras, o que von Neumann pretendia era estabelecer o análogo quântico da situação clássica, onde uma álgebra booleana pode ser interpretada tanto como a álgebra Tarski-Lindenbaum de uma lógica proposicional clássica como a estrutura algebraica que representa os eventos aleatórios de uma clássica teoria da probabilidade, sendo a probabilidade uma medida aditiva normalizada na álgebra booleana. [212, p. 157]

De fato, as dificuldades com uma definição rigorosa de probabilidade eram bem conhecidas por von Neumann [212]. Quando foi convidado para o Congresso de Matemáticos de 1954 realizado em Amsterdã, dedicado a problemas não resolvidos em matemática - em um sabor semelhante ao encontro de Paris de 1900, em que Hilbert deu sua famosa conferência - von Neumann esboçou sua conferência (não compartilhada) sobre o papel de anéis contínuos de operadores para uma melhor compreensão de QM, QL e probabilidade quântica [211]. As dificuldades com a definição de uma "boa medida" sobre a rede de Hilbert fizeram von Neumann abandonar o formalismo ortodoxo da QM no espaço de Hilbert, ao qual ele mesmo contribuiu muito e enfrentou a classificação dos fatores e suas funções de dimensão que levou ao assunto das álgebras de von Neumann.

Hoje em dia, a definição de probabilidade ainda enfrenta vários desafios e o assunto está em debate. Por um lado, digite II 1fator (aquele cuja estrutura de projeção é uma geometria contínua e, portanto, uma rede modular ortomodular conforme exigido pela definição de medida de probabilidade) não é uma estrutura adequada para representar eventos quânticos. Por outro lado, existem diferentes candidatos para definir a probabilidade condicional e não há um critério exclusivo para escolher entre eles [81, 209]. Com respeito à interpretação, a interpretação de freqüência é insustentável para todas as probabilidades não-comutativas [213]. Como Rédei observa, "ainda assim, uma interpretação satisfatória da medida não-comutativa como probabilidade e a relação dessa probabilidade não-comutativa (quântica) com a lógica (quântica) ainda falta". [211]

f. Potencialidade e Actualidade

Como discutimos acima, a QL tem sido relacionada à atualidade desde sua origem. A perspectiva operacionista de Birkhoff e von Neumann estava implicitamente relacionada ao problema de medição (MP). No QM ", uma descrição matemática completa de um sistema físico S não permite, em geral, prever com certeza o resultado de uma experiência". [41] De fato, a QM descreve matematicamente o estado em termos de superposição, portanto a questão levanta: por que observamos um único resultado (que corresponde a um único eigenstate) em vez de algo relacionado a uma superposição deles? Embora o MP aceite o fato de que há algo muito estranho sobre superposições quânticas, deixando de lado seu significado problemático, enfoca a justificativa do processo de atualização. Tomando como ponto de vista o resultado único, ele pergunta como chegamos ao resultado real da multiplicidade de estados possíveis. O MP é, portanto, uma tentativa de justificar o porquê, independentemente do QM, apenas observamos a realidade. O problema coloca o resultado na origem, o que precisa ser justificado é a resposta já conhecida.

QL distingue, em geral, as propriedades "reais" e as "possíveis" ou as "potenciais", abrindo a porta para discutir um reino de existência além da atualidade. A noção de potencialidade foi introduzida por Heisenberg no QM e, posteriormente, foi desenvolvida e relacionada através da abordagem operacionista da QL por Piron em [196] e mais recentemente por Aerts em [14, 15] (ver também para discussão [217]). Dentro de tais interpretações, o colapso é aceito e as potencialidades são definidas em termos de "tornar-se real". Uma noção diferente de potencialidade que tenta escapar dos limites da realidade também foi desenvolvida em [83, 84]. De acordo com essa abordagem, deve-se transformar as coisas de cabeça para baixo; não precisamos explicar o real através do potencial, mas sim, precisamos usar o real para desenvolver o potencial.

De perspectivas diferentes, o desenvolvimento da noção de potencialidade em QM está relacionado a uma tentativa de fornecer uma representação física realista da teoria que vá além do discurso sobre meros "resultados reais". Essas propostas estão em linha com a tentativa de entender o que é um superposição quântica, que é a principal ferramenta teórica que abriu a porta para os desenvolvimentos e experimentos tecnológicos mais destacados na física do início do século XXI .

6. Observações finais

A lógica quântica influenciou profundamente nossa compreensão da estrutura formal de QM. Também desempenhou um papel importante nos debates fundamentais sobre a teoria. No início do século XXI, o surgimento de uma nova era tecnológica fundamentada no processamento de informações quânticas está colocando questões e desafios originais para todos os pesquisadores próximos do campo. A este respeito, a pesquisa em curso na QL (seção 6) pode revelar-se um guia importante para tentar avançar nossa compreensão dos fenômenos implicados por essas tecnologias.

7. Bibliografia 

[1] Abramsky, S., 1996, "Retratando alguns caminhos em álgebra de processo", em Procedimentos de CONCUR 96, Notas de aula em Ciência da Computação, vol. 1119, 1-17, Springer-Verlag, Berlim. 
[2] Abramsky, S. e Coecke, B., 2008, "Mecânica quântica categórica", em Handbook of Quantum Logic e Quantum Structures, vol. II, K. Engesser, DM Gabbay e D. Lehmann (Eds.) Elsevier, Amsterdã. 
[3] Abramsky, S. e Coecke, B., 2004, "Semântica categórica de protocolos quânticos", em LICS Proceedings, 415-425. 
[4] Abramsky, S. e Duncan, RW, 2006, "Lógica quantitativa categórica", Estruturas matemáticas em informática, 16, 469-489. 
[5] Aerts, D. e Daubechies, I., 1979 "Uma caracterização de subsistemas em física", Letras em Física Matemática, 3, 11-17.
[6] Aerts, D. e Daubechies, I., 1979, "Uma condição matemática para um sublattice de um sistema proposicional para representar um subsistema físico, com uma interpretação física", Letters in Mathematical Physics, 3 19-27. 
[7] Aerts, D., 1981, The One and the Many: Rumo a uma unificação da descrição quântica e clássica de uma e muitas entidades físicas, dissertação de doutorado, Brussels Free University, Bélgica. 
[8] Aerts, D., 1981, "Descrição do sistema físico composto e interação lógica dos sistemas físicos", em Questões Atuais sobre Quantum Logic, EG Beltrametti e BC van Fraassen (Eds.), Pp. 381-405, Kluwer Academic Publishers, Dordrecht.
[9] Aerts, D., 1982, "Descrição de muitas entidades físicas sem os paradoxos encontrados na mecânica quântica", Foundations of Physics, 12, 1131-1170. 
[10] Aerts, D., 1983, "Teorias clássicas e teorias não clássicas como um caso especial de uma teoria mais geral", Journal of Mathematical Physics, 24, 24412453. 
[11] Aerts, D., 1984, "Construction de uma estrutura que permite descrever o sistema articular de um sistema clássico e um sistema quântico ", Reports in Mathematical Physics, 20, 421-428. 
[12] Aerts, D., 1999, "Fundamentos da física quântica: uma abordagem geral realista e operacional", International Journal of Theoretical Physics, 38, 289-358. 
[13] Aerts, D., 2009, "Estrutura quântica na cognição", Journal of Mathematical Psychology, 53, 314-348.
[14] Aerts, D., 2009, "Partículas quânticas como entidades conceituais: uma possível estrutura explicativa para a teoria quântica", Fundamentos da Ciência, 14, 361-411. 
[15] Aerts, D., 2010, "Uma potencialidade e conceitualidade da interpretação da mecânica quântica", Philosophica, 83, 15-52. 
[16] Aerts, D., 2011, "interferência quântica e superposição na cognição. Desenvolvimento de uma teoria para a disjunção de conceitos ", em visões do mundo, ciência e nós: Bridging Knowledge e suas implicações para nossas perspectivas do mundo, D. Aerts, J. Broekaert, B. D'Hooghe e N. Note (Eds. ), pp. 169-211, World Scientific, Singapura. 
[17] Aerts, D., Broekaert, J. e Gabora, L., 2011, "Um caso para aplicar um formalismo quântico abstraído à cognição", New Ideas in Psychology, 29, 136-146.
[18] Aerts, D., Czachor, M e Sozzo, S., 2011, "abordagem de interação quântica em cognição, inteligência artificial e robótica" em Procedimentos da Quinta Conferência Internacional sobre Quantum, Nano e Micro Technologies, V. Privman e V. Ovchinnikov (Eds.), Pp. 35-40, 2011 
[19] Aerts, D. e Sozzo, S., 2011, "Estruturas quânticas na cognição: por que e como os conceitos estão emaranhados", em Quantum Interaction Lecture Notes in Informática, 7052, 116-127. 
[20] Aerts, D. Gabora, L. e Sozzo, S., 2013, "Conceitos e suas dinâmicas: uma modelagem teórica quântica do pensamento humano", Topics in Cognitive Science, 5, 737-772. 
[21] Aerts, D. e Sozzo, S., 2014, "Emaranhamento quântico em combinação de conceitos", International Journal of Theoretical Physics, 53, 3587-3603.
[22] Amira, H., Coecke, B. e Stubbe, I., 1998, "Como os quantales emergem introduzindo a indução dentro da abordagem operacional", Helvetica Physica Acta, 71, 554-572. 
[23] Arenhart, JR e Krause, D., 2014, "Oposições na mecânica quântica", em New Dimensions of the Square of Opposition, J.-Y. Béziau e K. Gan-Krzywoszynska (Eds.), Pp. 337-356, Philosophia Verlag, Munique. 
[24] Arenhart, JR e Krause, D., 2014, "Contradição, Mecânica Quântica e Praça da Oposição", Logique et Analyze. 
[25] Arenhart, JR e Krause, D., 2015, "Potencialidade e contradição na mecânica quântica", em The Road to Universal Logic (volume II), A. Koslow e A. Buchsbaum (Eds.), Pp. 201- 211, Springer, Berlim.
[26] Bacciagaluppi, G., 1995, "A Kochen Specker Theorem na Interpretação Modal da Mecânica Quântica", Internal Journal of Theoretical Physics, 34, 1205-1216. 
[27] Bacciagaluppi, G. e Dickson, WM, 1997, "Dynamics for Density Operator Interpretations of Quantum Theory", Preprint. (quantph / arXiv: 9711048) 
[28] Baltag, A. e Smets, S., 2004, "A lógica dos programas quânticos", em Procedimentos do 2º Workshop Internacional sobre Linguagens de Programação Quântica, P. Selinger (Ed.), pp. 39-56, publicação geral do TUCS. 
[29] Baltag, A. e Smets, S., 2010, "Conhecimento correlacionado: uma visão lógica epistêmica sobre o emaranhamento quântico", Internal Journal of Theoretical Physics, 49, 3005-3021. 
[30] Baltag, A. e Smets, S., 2012, "A mudança dinâmica na lógica quântica", Synthese, 186, 753-773.
[31] Baltag, A., Bergfeld, J., Kishida, K., Sack, J., Smets, S. e Zhong, S., 2014, "PLQP e empresa: lógica determinável para algoritmos quânticos", Internal Journal of Física teórica, 53, 3628-3647. 
[32] Beltrametti, EG e Cassinelli, J., 1981, The Logic of Quantum Mechanics, Addison-Wesley, Reading, Nova York. 
[33] Beltrametti, EG e van Fraassen, BC (Eds.), 1981, Current Issues in Quantum Logic, Plenum, Nova York. 
[34] Beltrametti, E., Dalla Chiara, ML, Giuntini, R., Leporini, R. e Sergioli, G., 2014, "Uma semântica computacional quântica para operadores lógicos epistêmicos. Parte I: estruturas epistêmicas ", Internal Journal of Theoretical Physics, 53, 3279-3292.
[35] Beltrametti, E., Dalla Chiara, ML, Giuntini, R., Leporini, R. e Sergioli, G., 2014, "Uma semântica computacional quântica para operadores lógicos epistêmicos. Parte II: semântica ", Internal Journal of Theoretical Physics, 53, 3293-3307. 
[36] Bennett, MK e Foulis, DJ, 1995, "Álgebras de efeito simétrico Phi", Foundations of Physics, 25, 1699-1722. 
[37] Bennett, MK e Foulis, DJ, 1997, "Álgebras de Intervalos e lógicas quânticas de unsharp", Advances in Mathematics, 19, 200-215. 
[38] Béziau, J.-Y., 2003, "Nova luz no quadrado da oposição e seu canto sem nome", Logical Investigations, 10, 218-232. 
[39] Béziau, J.-Y., 2012, "The Power of the Hexagon", Logica Universalis, 6, 1-43.
[40] Béziau, J.-Y., 2014, "Lógica paraconsistente e ponto de vista contraditório", Revista Brasileira de Filosofia. 
[41] Birkhoff, G. e von Neumann, J., 1936, "A lógica da mecânica quântica", Annals of Mathematics 37, 823-843. 
[42] Bitbol, ​​M., 1996, Mécanique Quantique, Flamarion, Paris. 
[43] Bitbol, ​​M., 1998, "Alguns passos para uma dedução trascendental da mecânica quântica", Philosophia Naturalis, 35, 253-280. 
[44] Bohr, N., 1985, Collected Works, vol. 6, I. Kolckar (Ed.), Holanda do Norte, Amsterdã. 
[45] Brouwmeester, D., Ekert, AK e Zeilinger, A., 2001, The Physics of Quantum Information: Quantum Criptography, Quantum Teleportation, Quantum Computation, Springer, Berlim.
[46] Bub, J., 1992, "Mecânica Quântica Sem o Postulado de Projeção", Foundations of Physics, 22, 737-754. 
[47] Bub, J., 1997, Interpretando o Quantum World, Cambridge University Press, Cambridge. 
[48] ​​Bush, P., Pfarr, J., Ristig, M. e Stachow, E.-W., 2010, "QuantumMatter-Spacetime: as contribuições de Peter Mittelstaedt para a física e suas fundações", Foundations of Physics, 40, 1163 -1170. 
[49] Caleiro, C., Mateus, P., Sernadas, A. e Sernadas, C., 2006, "Instituições Quânticas", em Álgebra, Significado e Computação: Ensaios dedicados a Joseph A. Goguen por ocasião de Sua 65º aniversário, K. Futatsugi, J.-P. Jouannaud e J. Meseguer (Eds.), 50-64, Springer-Verlag, Berlim.
[50] Caspers, M., Heunen, C., Landsman, N. e Spitters, B., 2009, "Lógica quantitativa intuitiva de um sistema de n nível", Foundations of Physics, 39, 731-759. 
[51] Cattaneo, G. e Nisticò, G., 1986, "Brower-Zadeh posets e três-valorados? Ukasiewicz posets", Fuzzy Sets and Systems, 33, 165-190. 
[52] Cattaneo, G. e Laudisa, F., 1994, "Teoria quântica unsharp axiomática (de Mackey a Ludwig e Piron)", Foundations of Physics, 24, 631-683. 
[53] Cattaneo, G., Dalla Chiara, ML, Giuntini, R. e Leporini, R., 2004, "Uma lógica unsharp da computação quântica", International Journal of Theoretical Physics, 43, 1803-1817.
[54] Cattaneo, G., Dalla Chiara, ML, Giuntini, R. e Paoli, F., 2009, "Lógica Quântica e Lógica Não Clássica", no Manual de Lógica Quântica e Estruturas Quânticas, K. Engesser, D. Gabbay e D. Lehmann (Eds), pp. 127-226, Elsevier, Amsterdã. 
[55] Chajda, I. e Kühr, J., 2012, "Uma generalização de álgebras e ortótomos de efeitos", Mathematica Slovaca, 62, 1045-1062. 
[56] Clifton, RK, 1996, "The Properties of Modal Interpretations of Quantum Mechanics", British Journal for the Philosophy of Science, 47, 371-398. 
[57] Coecke, B., 2000, "Caracterização estrutural da composição", International Journal of Theoretical Physics, 39, 581-590.
[58] Coecke, B., Moore, DJ e Wilce, A., 2000, "Lógica Quantum Operacional: uma Visão Geral", em Pesquisa Atualizada em Lógica Quantitativa Operacional: Álgebras, Categorias, Idiomas, B. Coecke, DJ Moore e A Wilce (Eds.), Pp. 1-36, Kluwer Academic Publishers, Dordrecht. 
[59] Coecke, B., Moore, DJ e Stubbe, I., 2001, "Quantaloides descrevendo a causação e propagação de propriedades físicas", Foundation of Physics Letters, 14, 357-367. 
[60] Coecke, B. e Smets, S., 2004, "O Sasaki-hook não é um conectivo implicativo [estático], mas induz um dinâmico atrasado [no tempo] que atribui causas", International Journal of Theoretical Physics, 43 1705-1736.
[61] Coecke, B., Moore DJ e Wilce A. (Eds.), 2000, Pesquisa atual em lógica quantitativa operacional: Algebras Categorias, Idiomas, Kluwer Academic Publishers, Dordrecht. 
[62] Coecke, B., Moore, DJ e Smets, S., 2004, "Lógica de dinâmica e dinâmica da lógica", em Lógica, Epistemologia e Unidade de Ciências, S. Rahman, J. Symons (Eds.) , pp. 527-555, Kluwer Academic Publisher, Dordrecht. 
[63] Coecke, B., 2005, "Mecânica quântica do jardim de infância", em Procedimentos de QTRF-III, G. Adenier, A.Yu Khrennikov e TM Nieuwenhuizen (Eds.), Pp. 81-98, AIP Proceedings, New York . 
[64] Coecke, B., 2010, "Picturalismo Quântico", Contemporary Physics, 51, 5983.
[65] Coecke, B., Duncan, R., Kissinger, A. e Wang, Q., 2012, "Forte complementaridade e não localidade na mecânica quântica categórica", em Procedimentos do 27º Simpósio anual IEEE sobre lógica em computador Science LiCS 2012, pp. 245-254, IEEE Publisher. 
[66] Coecke, B., 2012, "The Logic of Quantum Mechanics - Take II", Preprint. (quant-ph / arXiv: 1204.3458) 
[67] Coecke, B., Heunen, C. e Kissinger, A., 2013, "Composição Quantum Logic", Computação, Lógica, Jogos e Fundações de Quantum, 21-36. 
[68] da Costa, NCA, 1997, Logique Classique et Non-Classique, Masson, Paris. 
[69] da Costa, NCA e French, S., 2003, Verdade Parcial: Uma Abordagem Unitária de Modelos e Raciocínio Científico, Oxford University Press, Oxford.
[70] da Costa, NCA, Krause, D. e Bueno, O., 2006, "Lógica Paraconsidente e Paraconsistência", na Filosofia da lógica, DM Gabbay, P. Thagard e J. Woods (Eds.), Pp. 655 -781, Elsevier, Amsterdã. 
[71] da Costa, NCA e Krause, D., 2006, "A lógica da complementaridade", na Era das Lógicas Alternativas: Avaliação da Filosofia da Lógica e Matemática Hoje, J. van Benthem, G. Heinzmann, M. Rebushi e H. Visser (Eds.), Pp. 103-120, Springer, Berlim. 
[72] da Costa, NCA, Krause, D. e Bueno, O., 2007, "Lógica Paraconsidente e Paraconsistência", no Manual da Filosofia da Ciência (Filosofia da Lógica), D. Jacquette (Ed.), Pp. 791-911, Elsevier, Amsterdã. 
[73] da Costa, NCA e Bueno, O., 2009, "Lógica não Reflexiva", Revista Brasilera de Filosofía, 232, 181-196.
[74] da Costa, N. e de Ronde, C., 2013, "The Paraconsistent Logic of Quantum Superpositions", Foundations of Physics, 43, 845-858. 
[75] da Costa, NCA e de Ronde, C., 2014, "Fundação Lógica Não Reflexiva para Mecânica Quântica", Fundamentos da Física, 44, 1369-1380. 
[76] da Costa, NCA e de Ronde, C., 2014, "A abordagem Paraconsistent às superposições quânticas recarregadas", Preprint. (Quantph / arXiv: 1507.02706) 
[77] Dalla Chiara, ML, Giuntini, R. e Krause, D., 1998, "Quasi set theories for microobjects: a comparison", em Interpreting Bodies: Classical and Quantum Objects in Modern Physics, E. Castellani (Ed.), Princeton University Press, Princeton.
[78] Dalla Chiara, M. e Giuntini, R., 2002, "Lógica quântica", no Handbook of Philosophical Logic, Vol. 6, D. Gabbay e F. Guenthner, (Eds.), Kluwer Academic Publishers, Dordrecht. 
[79] Dalla Chiara, M. e Giuntini, R., 2000, "Idéias paraconsistentes na lógica quântica", Synthese, 125, 55-68. 
[80] Dalla Chiara, ML, Giuntini, R. e Leporini, R., 2003, "Quantum Computational Logic". A Survey ", Preprint. (quant-ph / arXiv: 030529). 
[81] Dalla Chiara, M., Giuntini, R. e Greechie, R., 2004, Reasoning in Quantum Theory, Kluwer Academic Publishers, Dordrecht. 
[82] Dalla Chiara, ML, Giuntini, R., Freytes, H., Ledda, A. e Sergioli, G., 2009, "A Estrutura Algebraica de um Sistema Aproximadamente Universal de Portões Computacionais Quânticos", Fundação de Física, 39 , 559-572.
[83] de Ronde, C., 2011, O Caráter Contextual e Modal da Mecânica Quântica: Análise Formal e Filosófica nos Fundamentos da Física, dissertação de doutorado, Utrecht University, Utrecht. 
[84] de Ronde, C., 2013, "Superposições e Causalidade Quântica: Nos Vários Caminhos para o Resultado da Medida", Preprint. (Quantph / arXiv: 1310.4534) 
[85] de Ronde, C., 2013, "Representando superposições quânticas: potências, potencialidades e potencialidades", Preprint. (quant-ph / arXiv: 1312.7322) 
[86] de Ronde, C., 2015, "Modalidade, Potencialidade e Contradição na Mecânica Quântica", Novas Direções na Lógica Paraconsistente, pp. 249-265, J.-Y. Beziau, M. Chakraborty e S. Dutta (Eds.), Springer, Berlim.
[87] de Ronde, C., 2016, "Realismo representacional, teorias fechadas e limite quântico a clássico", em RE Kastner, J. Jeknic-Dugic e G. Jaroszkiewicz (Eds.), Quantum Structural Studies, World Scientific, Cingapura. 
[88] de Ronde, C., Freytes, H. e Domenech, G., 2014, "Interpretando o Teorema Modal de Kochen-Specker: Possibilidade e Muitos Mundos na Mecânica Quântica", Estudos em História e Filosofia da Física Moderna, 45, pp. 11-18. 
[89] de Ronde, C., Freytes, H. e Domenech, G., 2014, "Mecânica Quântica e Interpretação da Praça Oromodular da Oposição", em Novas Dimensões da Praça da Oposição, Jean-Yves Béziau e Katarzyna Gan-Krzywoszynska (Eds.), Pp. 223-242, Philosophia Verlag, Munique.
[90] DeWitt, B., 1973, "The Many-Universes Interpretation of Quantum Mechanics", In Foundations of Quantum Mechanics, 167-218, Academic Press, Nova York. 
[91] DeWitt, B. e Graham, N., 1973, The Many-Worlds Interpretation of Quantum Mechanics, Princeton University Press, Princeton. 
[92] Dickson, WM, 2001, "a lógica quântica está viva? (É verdade? É falso) ", Procedimentos da Filosofia da Associação de Ciência 2001, 3, S274-S287. 
[93] Dickson, WM, 1998, Chance quântica e não-localização: probabilidade e não-localização nas interpretações da mecânica quântica, Cambridge University Press, Cambridge.
[94] Dickson, M. e Dieks, D., 2002, "Interpretações Modais da Mecânica Quântica", a Enciclopédia da Filosofia de Stanford (edição de inverno 2002), EN Zalta (Ed.), URL: http: //plato.stanford .edu / archives / win2002 / entries / qm-modal /. 
[95] Dieks, D., 1988, "O formalismo da teoria quântica: uma descrição objetiva da realidade", Annalen der Physik, 7, 174-190. 
[96] Dieks, D., 1989, "Mecânica quântica sem o postulado de projeção e sua interpretação realista", Foundations of Physics, 19, 1397-1423. 
[97] Dieks, D., 2007, "Probabilidade na interpretação modal da mecânica quântica", Estudos em História e Filosofia da Física Moderna, 38, 292310. 
[98] Dieks, D., 2010, "Quantum Mechanics, Chance and Modalidade ", Philosophica, 83, 117-137.
[99] Dirac, PAM, 1974, The Principles of Quantum Mechanics, 4ª edição, Oxford University Press, Londres. 
[100] Domenech, G. e Freytes, H., 2005, "Lógica contextual para sistemas quânticos", Journal of Mathematical Physics, 46, 012102-1 - 012102-9. 
[101] Domenech, G. e Freytes, H., 2005, "Lógica proposicional difusa associada aos portões computacionais quânticos", International Journal of Theoretical Physics, 45, 228-261. 
[102] Domenech, G., Freytes, H. e de Ronde, C., 2006, "Escopos e limites da modalidade na mecânica quântica", Annalen der Physik, 15, 853-860. 
[103] Domenech, G., Freytes, H. e de Ronde, C., 2008, "Um estudo topológico de contextualidade e modalidade na mecânica quântica", International Journal of Theoretical Physics, 47, 168-174.
[104] Domenech, G., Freytes, H. e de Ronde, C., 2009, "lógica ortomodular de tipo modal", Mathematical Logic Quarterly, 3, 307-319. 
[105] Domenech, G., Freytes, H. e de Ronde, C., 2009, "Muitos mundos e modalidades na interpretação da mecânica quântica: uma abordagem algébrica", Journal of Mathematical Physics, 50, 072108. 
[106] Domenech, G., Holik, F e Massri, C., 2010, "Uma abordagem quântica lógica e geométrica para o estudo de misturas impróprias", Journal of Mathematical Physics, 51, 052108. 
[107] Döring, A. e Isham, CJ, 2008, "Fundação A topos para teorias da física: I. Línguas formais para a física", Journal of Mathematical Physics, 49, 053515.
[108] Döring, A. e Isham, CJ, 2008, "Fundação A topos para teorias da física: II. Daseinização e libertação da teoria quântica ", Journal of Mathematical Physics, 49, 053516. 
[109] Döring, A. e Isham, CJ, 2008," Fundação A topos para teorias da física: III. A representação de quantidades físicas com flechas ", Journal of Mathematical Physics, 49, 053517. 
[110] Döring, A. e Isham, CJ, 2008," Fundação A topos para teorias da física: VI. Categorias de sistemas ", Journal of Mathematical Physics, 49, 053518. 
[111] Döring, A. e Isham, CJ, 2011," O que é uma coisa "A teoria dos topos nos fundamentos da física", em Novas estruturas em física, B Coecke (Ed.), 753-940, Springer, Berlim.
[112] Dvure? Enskij, A. e Pulmannová, S., 1994, "Diferença posets, efeitos e medições quânticas", International Journal of Theoretical Physics, 33, 819-850. 
[113] Dvure? Enskij, A. e Pulmannová, S., 1994, "Tensor de produtos de D-posets e D-test spaces", Relatórios em Física Matemática, 34, 251-275. 
[114] Dvure? Enskij, A., 1995, "Tensor do produto da diferença de posets e álgebras de efeitos", International Journal of Theoretical Physics, 34, 1337-1348. 
[115] Dvure? Enskij A. e Pulmannova, S., 2000, Novas Tendências em Estruturas Quânticas, Kluwer Academic Publishers, Dordrecht. 
[116] Dvure? Enskij, A. e Xie, Y., 2014, "N-Perfect and Q-Perfect Pseudo Effect Algebras", International Journal of Theoretical Physics, 53, 33803390.
[117] Engesser, K., Gabbay, DM e Lehman, D. (Eds.), 2009, Handbook of Quantum Logic e Quantum Structures, Elsevier, Amsterdam. 
[118] Everett, H., 1957, "Formulação do Estado Relativo da Mecânica Quântica", Revisões da Modern Physics, 29, 454-462. 
[119] Everett, H., 1973, "The Theory of the Universal Wave Function", na interpretação de muitos mundos da mecânica quântica, DeWitt e Graham (Eds.), Princeton University Press, Princeton. 
[120] Finkelstein, D., "Matéria, espaço e lógica", em Boston Studies in the Philosophy of Science V, RS Cohen e MW Wartofsky (Eds.), D. Reidel, Dordrecht. 
[121] Finkelstein, D., "A física da lógica", em paradigmas e paradoxos: o desafio filosófico do domínio quântico, RG Colodny (Ed.), University of Pittsburg Press, Pittsburg.
[122] Foulis, DJ e Randall, CH, 1972, "Estatísticas operacionais, I. Conceitos básicos", Journal of Mathematical Physics, 13, 1667-1675. 
[123] Foulis, DJ e Randall, CH, 1974, "Lógica empírica e mecânica quântica", Synthese, 29, 81-111. 
[124] Foulis, DJ e Randall, CH, 1978, "Manuais, morfismos e mecânica quântica", em Fundamentos Matemáticos da Teoria Quântica, A. Marlow (Ed.), Academic Press, Nova York. 
[125] Foulis, DJ e Randall, CH, 1979, "Os produtos Tensor de lógicas quânticas não existem", Noticies of the American Mathematical Society, 26, 557. 
[126] Foulis, DJ e Randall, CH, 1981, "Empírico produtos de lógica e tensores ", em Interpretações e Fundamentos da Teoria Quântica, H. Neumann (ed.), BI Wissenschaft, Mannheim.
[127] Foulis, DJ, Piron, C. e Randall, CH, 1983, "Realismo, Operacionalismo e Mecânica Quântica", Fundamentos da Física, 13, 813-841. 
[128] Foulis, DJ e Bennett, MK, 1994, "Álgebras de efeitos e lógicas quânticas de unsharp", Foundations of Physics, 24, 1331-1352. 
[129] Foulis, DJ, Bennett, MK e Greechie, RJ, 1996, "Grupos de teste e álgebras de efeitos", International Journal of Theoretical Physics, 35, 11171140. 
[130] Foulis, DJ, 2000, "Representations on unigroups", em Pesquisa atual em Lógica Quantum Operacional: Algebras Categorias, Idiomas, B. Coecke, DJ Moore e A. Wilce (Eds.), Kluwer Academic Publishers, Dordrecht.
[131] Foulis, DJ, Pulmannová, S. e Vinceková, E., 2011, "Álgebras de pseudo-efeito de estrutura como estruturas duplas residuadas", Soft Computing, 15, 24792488. 
[132] Foulis, DJ e Pulmannová, S., 2013, "Teoria da dimensão para álgebras de efeitos generalizados", Algebra Universalis, 69, 357-386. 
[133] Foulis, DJ e Pulmannová, S., 2014, "Simetrias em álgebras sinápticas", Mathematica Slovaca, 64, 751-776. 
[134] Francês, S. e Krause, D., 2006, Identidade em Física: Análise Histórica, Filosófica e Formal, Oxford University Press, Oxford. 
[135] Freytes, H. e Ledda, A., 2009, "Categorias de semigrupos em estruturas computacionais quânticas", Mathematica Slovaca, 59, 413-432
[136] Freytes, H., 2010, "Estruturas computacionais quânticas: equivalência categórica para álgebras QMV de raízes quadradas", Studia Logica, 95, 63-80. 
[137] Freytes, H., de Ronde, C. e Domenech, G., 2012, "A Praça da Oposição na Lógica Ortomodular", em Around and Beyond the Square of Opposition: Studies in Universal Logic, J.-Y. Béziau e D. Jacquette (Eds.), Pp. 193-201, Springer, Basileia. 
[138] Freytes, H. e Domenech, G., 2013, "Lógica computacional quântica com estados mistos", Mathematical Logic Quarterly, 59, 27-50. 
[139] Friedman, M. e Putnam, H., 1978, "Lógica quântica, probabilidade condicional e inferência", Dialectica, 32, 305-315. 
[140] Girard, JY, "Linear logic", 1987, Theoretical Computational Science, 50, 1-102.
[141] Giuntini, R. e Greuling, H., 1989, "Rumo a uma linguagem formal para propriedades unsharp", Foundations of Physics, 19, 931-945. 
[142] Giuntini, R., 1996, "Quantum MV-Algebras", Studia Logica, 56, 393-417. 
[143] Giuntini, R., Freytes, H. Ledda, A. e Paoli, F., 2009, "Uma variedade discriminadora de álgebras Gödel com operadores provenientes de computação quântica", Fuzzy Sets and Systems, 160, 1082-1098. 
[144] Gleason, AM, 1957, "Medidas sobre os subespaços fechados de um espaço de Hilbert", Journal Mathematical Mechanics, 6, 885-893. 
[145] Goldblatt, RI, 1974, "Análise semântica de ortográficos", Journal of Philosophical Logic, 3, 19-35. 
[146] Goldblatt, RI, 1984, Topoi: A análise categorial da lógica, Elsevier, Amsterdã.
[147] Greechie, RJ, Foulis, DJ e Pulmannová, S., 1995, "O centro de uma álgebra de efeito", Order, 12, 910-106. 
[148] Gudder, SP, "Effect test spaces", 1997, International Journal of Theoretical Physics, 36, 2681-2705. 
[149] Gudder, S., 2002, "Quantum Computational Logic", International Journal of Theoretical Physics, 42, 39-47. 
[150] Halmos, P., 1995, "Lógica algébrica I, álgebras boadianas monádicas", Compositio Mathematica, 12, 217-249. 
[151] Hajek, P., 1998, Metamathematics of Fuzzy Logic, Kluwer Academic Publishers, Dordrecht. 
[152] Heisenberg, W., 1958, Física e Filosofia, Ruskin House, Londres.
[153] Heisenberg, W., 1973, "Desenvolvimento de conceitos na história da teoria quântica", na Conceição da Natureza do Físico, 264-275, J. Mehra (Ed.), Reidel, Dordrecht. 
[154] Heunen, C. e Spitters, B., 2009, "A Topos para a Teoria quântica algébrica", Communications in Mathematical Physics, 291, 63-110. 
[155] Hooker, CA (Ed.), 1979, A Abordagem Logico-Algebraica da Mecânica Quântica II, D. Reidel, Dordrecht. 
[156] Husimi, K., 1937, "Estudos sobre os fundamentos da mecânica quântica I", Proceedings of the Physico-Mathematical Society Japan, 9, 766-778. 
[157] Isham, CJ, 2011, "Topos Methods in the Foundations of Physics", em Deep Beauty, H. Halvorson (Ed.), 187-206, Cambridge University Press. 
[158] Jammer, M., 1974, Philosophy of Quantum Mechanics, Wiley, Nova York.
[159] Jauch, JM, 1968, Fundações da Mecânica Quântica, Addison-Wesley, Reading. 
[160] Jauch, JM e Piron, C., 1969, "Sobre a estrutura dos sistemas de proposição quântica", Helvetica Physica Acta, 42, 842-848. 
[161] Kalman, JA, 1958, "Lattice with involution", Transactions of the American Mathematical Society, 87, 485-491. 
[162] Kalmbach, G., 1983, Lattes Ortomodulares, Academic Press, Londres. 
[163] Kauark-Leite, P., 2004, A Abordagem Transcendental e o Problema de Linguagem e Realidade em Mecânica Quântica, Dissertação de Mestrado, Centro de Pesquisa em Epistemologia Aplicada - École Polytechnique, Paris. 
[164] Kaye, P., Laflamme, R. e Mosca, M., 2007, Uma introdução à computação quântica, Oxford University Press, Nova York.
[165] Kissinger, A., 2014, "Abstract Tensor Systems as Monoidal Categories", em Categorias e Tipos em Lógica, Linguagem e Física, 235-252. 
[166] Kochen, S., 1985, "Uma nova interpretação da mecânica quântica", no Simpósio sobre os fundamentos da Modern Physics 1985, P. Lathi e P. Mittelslaedt (Eds.), Pp. 151-169, World Scientific, Johensuu. 
[167] Kochen, S. e Specker, E., 1967, "Sobre o problema das variáveis ​​ocultas na mecânica quântica", Journal of Mathematics and Mechanics, 17, 59-87. Reimpresso em Hooker, 1975, 293-328. 
[168] Köhler, P., 1981, "semanais Brouwerian", Transações da American Mathematical Society, 268, 103-126. 
[169] Kôpka, F., 1992, "D-posets de conjuntos difusos", Tatra Mountains Mathematical Publications, 1, 83-87.
[170] Krause, K., 1992, "Sobre uma teoria quase definida", Notre Dame Journal of Formal Logic, 33, 402-411. 
[171] Krause, D., 2002, "Por quê?", Boletim da Sociedade Paranaense de Matemática, 20, 73-92. 
[172] Krause, D., 2014, "O problema da identidade e uma justificativa para uma mecânica quântica não-reflexiva", Lógica Journal of the IGLP, 22, 186-205. 
[173] Krause, D. e Arenhart, J., 2016, "Uma lógica de superposições quânticas", em Probing the Meaning of Quantum Mechanics, D. Aerts, C. de Ronde, H. Freytes e R. Giuntini (Eds. ), World Scientific, Singapura. 
[174] Lahti, P., 1980, "Incerteza e complementaridade na mecânica quântica axiomática", International Journal of Theoretical Physics, 19, 789-842.
[175] Lewis, D., 1986, sobre a pluralidade dos mundos, Blackwell Publishers, Harvard. 
[176] Ludwig, G., Uma base axiomática da mecânica quântica 1. Derivação do espaço de Hilbert, Springer-Verlag, Berlim, 1985 
[177] Ludwig, G., 1987, Uma fundação axiomática da mecânica quântica 2. Mecânica quântica e macrosistemas , Springer-Verlag, Berlim. 
[178] Lyre, H., 2003, "Reconstrução de Física de von Weizsäcker: ontem, hoje, amanhã", no tempo, quantum e informação (Ensaios em honra de CF von Weizsäcker), L. Castell e O. Ischebeck (Eds .), Springer, Berlim. 
[179] Mackey, GW, 1963, The Mathematical Foundations of Quantum Mechanics, Benjamin, Amsterdã. 
[180] Maeda, F. e Maeda, S., 1970, Teoria das retas simétricas, SpringerVerlag, Berlim.
[181] Manin, Yu.I., 1976, "Problemas matemáticos I: Fundações", em Problemas Matemáticos decorrentes de Problemas de Hilbert, FE Browder (Ed.), P. 36, American Mathematical Society, Providence. 
[182] Mateus P. e Sernadas, A., 2004, "Reasoning About Quantum Systems", em Lógica em Inteligência Artificial, Nona Conferência Européia, JELIA-04, 239-251, J. Alferes e J. Leite (Eds), Springer-Verlag. 
[183] ​​Mateus P. e Sernadas, A., 2006, "Axiomatização fraca e completa da lógica proposicional quântica exógena", Information and Computation, 204, 771-794. 
[184] Matoušek, M. e Pták, P., 2014, "Posets ortomodulares relacionados aos estados zvalados", International Journal of Theoretical Physics, 53, 3323-3332 [185] Mittelstäedt; P., 1978, lógica quântica, Reidel, Dordrecht.
[186] Mittelstäedt; P. 1979, "A lógica modal da lógica quântica", Journal Philosophical Logic, 8, 479-504. 
[187] Mittelstäedt; P., 1981, "Os conceitos de verdade, possibilidade de uma probabilidade na linguagem da física quântica", em Interpretações e Fundamentos da Teoria Quântica, H. Neumann (Ed.), Pp. 70-94, Bibliographisches Institut, Mannheim. 
[188] Mittelstäedt; P. 1981, "A abordagem dialógica das modalidades na linguagem da física quântica", em Questões Atuais na Lógica Quântica, E. Beltrametti e BC van Fraassen (Eds.), Pp. 259-281, Plenum Publication Co, Nova York . 
[189] Mittelstäedt; P., 1985, "Constituição, Nomeação e Identidade na Lógica Quântica", em Desenvolvimentos Recentes na Lógica Quântica, P. Mittelstäedt e E.-W. Statchow (Eds.), Pp. 215-234, BI-Wissenschaftsverlag, Mannheim.
[190] Mittelstäedt; P., 1986, "Nomeação e Identidade na Lógica Quântica", em Fundamentos da física, P. Weingartner e G. Dorn (Eds.), Pp. 139-161, Viena. 
[191] Nielsen, MA e Chuang, IL, 2010, Computação Quântica e Informação Quântica: edição do 10º aniversário, Cambridge University Press, Cambridge. 
[192] Paoli, F., Ledda, A., Giuntini, R. e Freytes, H., 2009, "Em algumas propriedades de álgebras quasi-MV e álgebras quasi-MT MVR", Relatórios sobre Lógica Matemática, 44, 31 -63. 
[193] Paoli, F., Ledda, A., Spinks, Freytes, H. e Giuntini, R., 2011, "Lógica de sqrt MV-álgebras", International Journal of Theoretical Physics, 50, 3882-3902. 
[194] Piron, C., 1964, "Axiomatique Quantique", Helvética Physica Acta, 37, 439-468.
[195] Piron, C., 1976, Fundações da Mecânica Quântica, WA Benjamin, Inc., Reading. 
[196] Piron, C., 1983, "O realismo em físico quantita: uma abordagem selon Aristote", No conceito de realidade física. Procedimentos de uma conferência organizada pelo Grupo de pesquisa interdisciplinar, Universidade de Atenas, Atenas. 
[197] Piron, C., 1989, "Desenvolvimentos Recentes na Mecânica Quântica", Helvética Physica Acta, 62, 82-90. 
[198] Pták, P. e Pulmannová, S., 1991, Estruturas Ortomodulares como Lógica Quântica, Kluwer Academic Publishers, Dordrecht. 
[199] Pulmannová, S., 1985, "Tensor Produto de Lógica Quântica", Journal of Mathematical Physics, 26, 1-5.
[200] Pulmannová, S. e Wilce, A., 1995, "Representações de D-posets", International Journal of Theoretical Physics, 34, 1689-1696. 
[201] Pulmannová, S. e Vincenková, E., 2007, "Observações sobre a ordem de observações quânticas", Mathematica Slovaca, 57, 589-600. 
[202] Putnam, H., 1968, "É lógica empírica?", Boston Studies in the Philosophy of Science V, 5, 199-215. 
[203] Putnam, H., 1974, "How To Think Quantum Logically", Synthese, 29, 55-61. 
[204] Randall CH e Foulis, DJ, 1970, "Uma abordagem à lógica empírica", American Mathematicl Monthly, 77, 363-374. 
[205] Randall CH e Foulis, DJ, 1973, "Estatísticas operacionais II. Manuais de operações e suas lógicas ", Journal Mathematical Physics, 14, 1472-1480.
[206] Randall CH e Foulis, DJ, 1983, "Uma linguagem matemática para a física quântica", em Les fondements de la mécanique quantique, C. Gruber, C. piron, TM Tâm e R. Weil (Eds), AVCP, Lausanne . 
[207] Randall, CH e Foulis, DJ, 1983, "Propriedades e proposições operacionais na mecânica quântica", Foundations of Physics, 13, 843-857. 
[208] Reichenbach, H., 1975, "Três lógicas valiosas e a interpretação da mecânica quântica", na Abordagem Lógico-Algebraica da Mecânica Quântica - Vol I, CA Hooker (Ed.), Reidel, Dordrecht. 
[209] Rédei, M., 1989, "As probabilidades condicionais quânticas não são probabilidades de contingência quântica", Physics Letters, A 139, 287-290. 
[210] Rédei, M., 1998, lógica quântica em abordagem algébrica, Kluwer Academic Publishers, Dordrecht.
[211] Rédei, M., 1999, "Problemas não resolvidos da Matemática" Discurso de J. von Neumann ao Congresso Internacional de Matemáticos, Amsterdã, 2-9 de setembro de 1954 ", The Mathematical Intelligencer, 21, 7-12. 
[212] Rédei, M., 2001, "O conceito de Von Neumann da lógica quântica e da probabilidade quântica", em John von Neumann e os Fundamentos da Física Quântica, M. Rédei e M. Stötzner (Eds.), Pp. 153-172. , Kluwer Academic Publishers, Dordrecht. 
[213] Rédei, M. e Summers, SJ, 2007, "Teoria da probabilidade quântica", Estudos na História e Filosofia da Física Moderna, 38, 390-417. 
[214] Sakurai, JJ e Napolitano, J., 2010, Modern Quantum Mechanics, Addison-Wesley, Londres. 
[215] Smets, S., 2000, "Em Defesa da Lógica Quântica Operacional", Lógica e Filosofia Lógica.
[216] Smets, S., 2001, A lógica das propriedades físicas na perspectiva estática e dinâmica, dissertação de doutorado, Brussels Free University, Bruxelas. 
[217] Smets, S., 2005, "Os Modos das Propriedades Físicas nos Fundamentos Lógicos da Física", Lógica e Filosofia Lógica, 14, 37-53. 
[218] Smets, S., 2010, "Lógica e física quântica", Journal of the Indian Council of Philosophical Research Spetial Issue XXVIII, N2. 
[219] Solèr, MP, 1995, "Caracterização dos espaços de Hilbert pelos espaços ortodomáticos", Communcations in Algebra, 23, 219-243. 
[220] Svozil, K., 1998, Quantum Logic, Springer, Singapura. 
[221] Takeuti, G., 1978, Duas Aplicações de Lógica para Matemática, Iwanami e Princeton University Press, Tóquio e Princeton.
[222] Takeuti, G., 1981, "Quantum Set Theory", em Questões Atuais em Quantum Logic, E. Beltrametti e BC van Frassen (Eds.), Pp. 303-322, Plenum, Nova York. 
[223] Titani, S., 1999, "Lattice Valued Set Theory", Archive for Mathematical Logic, 38, 395-421. 
[224] Van Fraassen, BC, 1972, "Uma abordagem formal para a filosofia da ciência", em Paradigmas e paradoxos: o desafio filosófico do domínio quântico, R. Colodny (Ed.), Pp. 303-366, Universidade de Pittsburgh Press, Pittsburgh. 
[225] Van Fraassen, BC, 1973, "Análise Semântica da Lógica Quântica", In Contemporary Research in the Foundations and Philosophy of Quantum Theory, CA Hooker (Ed.), Pp. 80-113, Reidel, Dordrecht. 
[226] Van Fraassen, BC, 1974, "O paradoxo de Einstein-Podolsky-Rosen", Synthese, 29, 291-309.
[227] Van Fraassen, BC, 1981, "Interpretação modal da mecânica quântica", em Questões atuais na lógica quântica, 229-258, EG Beltrametti e BC van Fraassen (Eds.), Plenum, Nova York. 
[228] Van Fraassen, BC, 1991, Mecânica quântica: uma visão empirista, Clarendon, Oxford. 
[229] Varadarajan, VS, 1962, "Probabilidade em Física e Teorema de Observabilidade Simultânea", Comunicação de Matemática Pura e Aplicada, XV, 189-217. 
[230] Varadarajan, VS, 1985, Geometria da Teoria Quântica, Springer, Berlim.
[231] Verelst, K. e Coecke, B., 1999, "Pensamento e perspectivas gregas precoce para a interpretação da mecânica quântica: Preliminares para uma abordagem ontológica", no Livro azul de Einstein Atende Magritte, Gustaaf C. Cornelis, Sonja Smets, Jean-Paul van Bendegem (Eds.), Pp. 163-196, Kluwer Academic Publishers, Dordrecht. 
[232] Vermaas, PE, 1999, A Philosophers Understanding of Quantum Mechanics, Cambridge University Press, Cambridge. 
[233] Vermaas, PE e Dieks, D., 1995, "A Interpretação Modal da Mecânica Quântica e sua Generalização para Operadores de Densidade", Foundations of Physics, 25, 145-158. 
[234] Von Neumann, J., 1996, Fundamentos Matemáticos da Mecânica Quântica, Princeton University Press (12ª edição), Princeton.
[235] Von Neumann, J., 1961, Collected Works Vol III: Rings of Operators, AH Taub (Ed.), Pergamon Press. 
[236] Von Weizsäcker, CF, 1985, "Filosofia de Heisenberg", no Simpósio sobre os Fundamentos da Física Moderna de 1985, P. Lathi e P. Mittelslaedt (Eds.), Pp. 277-293, World Scientific, Singapura. 
[237] Wilce, A., 1995, "Partiel Abelian Semigroups", International Journal of Theoretical Physics, 34, 1807-1812. 
[238] Wilce, A., 1998, "Perspectiva e Congruência em Semigrupos Partiel Abelianos", Mathematica Slovaca, 48, 117-135. 
[239] Zafiris, E. e Karakostas, V., 2013, "Uma representação semântica categorial de eventos quânticos", Foundations of Physics, 43, 1090-1123.