LÓGICA MODAL: PARTE 2
LÓGICA MODAL
UMA INTRODUÇÃO METATEÓRICA (PARTE 2)
VINICIUS DIAS DE SOUZA
LÓGICA MODAL
UMA INTRODUÇÃO METATEÓRICA (PARTE 2)
VINICIUS DIAS DE SOUZA
5. Listas de condição e relevância
O fundador da lógica modal, CI Lewis, definiu uma série de lógicas modais que não tinham □ como um símbolo primitivo. Lewis estava preocupado em desenvolver uma lógica de condicionamentos que fosse livre dos chamados Paradoxos de Implicação de Materiais, ou seja, os teoremas clássicos A → (~ A → B ) e B → ( A → B ). Ele apresentou o símbolo 
de "implicação rigorosa" e desenvolveu lógicas onde nem A (~ A B ) nem B (A B ) são prováveis. A prática moderna tem sido definir A B por □ ( A → B), e use lógica modal que regula □ para obter resultados semelhantes. No entanto, a provabilidade de fórmulas como ( A & ~ A ) B em tais lógicas parece estar em desacordo com a preocupação com os paradoxos. Anderson e Belnap (1975) desenvolveram sistemas R (para Lógica de Relevância) e E (para Entailment) que são projetados para superar tais dificuldades. Esses sistemas exigem a revisão dos sistemas padrão de lógica proposicional. (Ver Mares (2004) e a entrada na lógica de relevância .)
David Lewis (1973) e outros desenvolveram lógicas condicionais para lidar com expressões contrafactual, ou seja, expressões da forma 'se A fosse acontecer, então B seria acontecer'. (Kvart (1980) é outra boa fonte sobre o assunto.) As lógicas contrárias ao cliente diferem das baseadas em implicações estritas porque as primeiras rejeitam enquanto as últimas aceitam a contraposição.
O fundador da lógica modal, CI Lewis, definiu uma série de lógicas modais que não tinham □ como um símbolo primitivo. Lewis estava preocupado em desenvolver uma lógica de condicionamentos que fosse livre dos chamados Paradoxos de Implicação de Materiais, ou seja, os teoremas clássicos A → (~ A → B ) e B → ( A → B ). Ele apresentou o símbolo de "implicação rigorosa" e desenvolveu lógicas onde nem A (~ A B ) nem B (A B ) são prováveis. A prática moderna tem sido definir A B por □ ( A → B), e use lógica modal que regula □ para obter resultados semelhantes. No entanto, a provabilidade de fórmulas como ( A & ~ A ) B em tais lógicas parece estar em desacordo com a preocupação com os paradoxos. Anderson e Belnap (1975) desenvolveram sistemas R (para Lógica de Relevância) e E (para Entailment) que são projetados para superar tais dificuldades. Esses sistemas exigem a revisão dos sistemas padrão de lógica proposicional. (Ver Mares (2004) e a entrada na lógica de relevância .)
de "implicação rigorosa" e desenvolveu lógicas onde nem A (~ A B ) nem B (A B ) são prováveis. A prática moderna tem sido definir A B por □ ( A → B), e use lógica modal que regula □ para obter resultados semelhantes. No entanto, a provabilidade de fórmulas como ( A & ~ A ) B em tais lógicas parece estar em desacordo com a preocupação com os paradoxos. Anderson e Belnap (1975) desenvolveram sistemas R (para Lógica de Relevância) e E (para Entailment) que são projetados para superar tais dificuldades. Esses sistemas exigem a revisão dos sistemas padrão de lógica proposicional. (Ver Mares (2004) e a entrada na lógica de relevância .)
David Lewis (1973) e outros desenvolveram lógicas condicionais para lidar com expressões contrafactual, ou seja, expressões da forma 'se A fosse acontecer, então B seria acontecer'. (Kvart (1980) é outra boa fonte sobre o assunto.) As lógicas contrárias ao cliente diferem das baseadas em implicações estritas porque as primeiras rejeitam enquanto as últimas aceitam a contraposição.
6. Semântica dos mundos possíveis
O objetivo da lógica é caracterizar a diferença entre argumentos válidos e inválidos. Um sistema lógico para um idioma é um conjunto de axiomas e regras projetadas para provar exatamente os argumentos válidos que podem ser indicados no idioma. Criar essa lógica pode ser uma tarefa difícil. O lógico deve certificar-se de que o sistema é sólido , ou seja, que cada argumento comprovado usando as regras e os axiomas é de fato válido. Além disso, o sistema deve estarcompleto , o que significa que cada argumento válido tem uma prova no sistema. Demonstrar a solidez e a integridade dos sistemas formais é uma preocupação central do lógico.
Tal demonstração não pode ser iniciada até que o conceito de validade seja definido com rigor. A semântica formal para uma lógica fornece uma definição de validade, caracterizando o comportamento da verdade das frases do sistema. Na lógica proposicional, a validade pode ser definida usando tabelas de verdade. Um argumento válido é simplesmente aquele em que toda linha da tabela verdadeira que torna suas premissas verdadeiras também faz sua conclusão verdadeira. No entanto, as tabelas de verdade não podem ser usadas para fornecer uma conta de validade nas lógicas modais porque não há tabelas de verdade para expressões como "é necessário que", "é obrigatório que", e assim por diante. (O problema é que o valor de verdade de A não determina o valor de verdade para □ A. Por exemplo, quando A é 'Cães são cães', □ Aé verdade, mas quando A é "Cães são animais de estimação", □ A é falso.) No entanto, a semântica para as lógicas modal pode ser definida pela introdução de mundos possíveis. Vamos ilustrar possíveis semânquias mundiais para uma lógica de necessidade contendo os símbolos ~, → e □. Então, explicaremos como a mesma estratégia pode ser adaptada a outras lógicas da família modal.
Na lógica proposicional, uma avaliação das orações atômicas (ou linha de uma tabela de verdade) atribui um valor de verdade ( T ou F ) a cada variável proposicional p . Então, os valores de verdade das orações complexas são calculados com tabelas de verdade. Na semântica modal, um conjunto W de mundos possíveis é introduzido. A valorização, em seguida, dá um valor de verdade para cada variável proposicional para cada um dos mundos possíveis em W . Isso significa que o valor atribuído a p para o mundo w pode diferir do valor atribuído a p para outro mundo w '.
O valor de verdade da sentença atômica p no mundo w dado pela avaliação v pode ser escrito v ( p, w ). Dada esta notação, os valores de verdade ( T para true, F for false) de orações complexas de lógica modal para uma avaliação dada v (e membro w do conjunto de mundos W ) podem ser definidos pelas seguintes cláusulas de verdade. ('iff' abreviado 'se e somente se'.)
(~) V (~ A , w ) = T sse v ( A , w ) = F .
(→) v ( A → B , w ) = T sse v ( A , w ) = F ou v ( B , w ) = T .
(5) v (□ A , w ) = T sse para cada mundo w 'em W , v ( A , W ') = t .
Cláusulas (~) e (→) simplesmente descrevem o comportamento padrão da tabela de verdade para negação e implicação material, respectivamente. De acordo com (5), □ A é verdadeira (em um mundo w ) exatamente quando A é verdade em todos os mundos possíveis. Dada a definição de ◊, (a saber, ◊ A = ~ □ ~ A ), a condição de verdade (5) assegura que ◊ A é verdade apenas no caso de A ser verdade em algum mundo possível. Uma vez que as cláusulas de verdade para □ e ◊ envolvem os quantificadores "todos" e "alguns" (respectivamente), serão esperados paralelos no comportamento lógico entre □ e ∀ x , e entre ◊ e ∃ x observados na seção 2.
Cláusulas (~), (→) e (5) permitem calcular o valor de verdade de qualquer frase em qualquer mundo em uma determinada avaliação. Uma definição de validade está agora ao virar da esquina. Um argumento é 5-válido para um determinado conjunto W (de mundos possíveis) se e somente se cada avaliação das orações atômicas que atribuem as premissas T em um mundo em W também atribui a conclusão T no mesmo mundo. Um argumento é dito ser 5 válido se for válido para todos os conjuntos não vazios W de mundos possíveis.
Foi mostrado que S5 é som e completo para validade 5 (daí o uso do símbolo '5'). Os argumentos válidos em 5 são exatamente os argumentos prováveis no S5 . Este resultado sugere que S5 é a maneira correta de formular uma lógica de necessidade.
No entanto, S5 não é uma lógica razoável para todos os membros da família modal. Na lógica deontica, lógica temporal e outros, o análogo da condição de verdade (5) claramente não é apropriado; Além disso, há mesmo concepções de necessidade onde (5) deve ser rejeitado também. O ponto é mais fácil de ver no caso da lógica temporal. Aqui, os membros de W são momentos de tempo, ou mundos "congelados", por assim dizer, em um instante. Para simplificar, vamos considerar um futuro lógica temporal, uma lógica onde □ A lê: 'ele vai ser sempre o caso que'. (Nós formulamos o sistema usando □ em vez do tradicional Gde modo que as conexões com outras lógicas modais sejam mais fáceis de apreciar.) A cláusula correta para □ deve dizer que □ A é verdadeira no tempo w se A é verdade em todo o tempo no futuro de w. Para restringir a atenção para o futuro, a relação R (para 'eRlier than') precisa ser introduzida. Então, a cláusula correta pode ser formulada da seguinte forma.
( K ) v (□ A , w ) = T sse para cada w ', se w R w ', em seguida, v ( A , W ') = t .
Isso diz que □ A é verdade em w , caso o A seja verdadeiro em todos os momentos depois de w .
A validade para esta marca de lógica temporal agora pode ser definida. Um quadro < W , R > é um par que consiste de um conjunto não vazio W (de mundos) e uma relação binária R em W . Um modelo < F , v > consiste de um quadro F , e uma valorização v que atribui valores de verdade para cada sentença atômica em cada mundo em W . Dado um modelo, os valores de todas as orações complexas podem ser determinados usando (~), (→) e ( K ). Um argumento é K- valido apenas no caso de qualquer modelo cuja avaliação atribua as premissas TEm um mundo também atribui a conclusão T no mesmo mundo. Como o leitor pode ter adivinhado com o uso de ' K ', demonstrou-se que a lógica modal mais simples K é som e completa para a validade K.
O objetivo da lógica é caracterizar a diferença entre argumentos válidos e inválidos. Um sistema lógico para um idioma é um conjunto de axiomas e regras projetadas para provar exatamente os argumentos válidos que podem ser indicados no idioma. Criar essa lógica pode ser uma tarefa difícil. O lógico deve certificar-se de que o sistema é sólido , ou seja, que cada argumento comprovado usando as regras e os axiomas é de fato válido. Além disso, o sistema deve estarcompleto , o que significa que cada argumento válido tem uma prova no sistema. Demonstrar a solidez e a integridade dos sistemas formais é uma preocupação central do lógico.
Tal demonstração não pode ser iniciada até que o conceito de validade seja definido com rigor. A semântica formal para uma lógica fornece uma definição de validade, caracterizando o comportamento da verdade das frases do sistema. Na lógica proposicional, a validade pode ser definida usando tabelas de verdade. Um argumento válido é simplesmente aquele em que toda linha da tabela verdadeira que torna suas premissas verdadeiras também faz sua conclusão verdadeira. No entanto, as tabelas de verdade não podem ser usadas para fornecer uma conta de validade nas lógicas modais porque não há tabelas de verdade para expressões como "é necessário que", "é obrigatório que", e assim por diante. (O problema é que o valor de verdade de A não determina o valor de verdade para □ A. Por exemplo, quando A é 'Cães são cães', □ Aé verdade, mas quando A é "Cães são animais de estimação", □ A é falso.) No entanto, a semântica para as lógicas modal pode ser definida pela introdução de mundos possíveis. Vamos ilustrar possíveis semânquias mundiais para uma lógica de necessidade contendo os símbolos ~, → e □. Então, explicaremos como a mesma estratégia pode ser adaptada a outras lógicas da família modal.
Na lógica proposicional, uma avaliação das orações atômicas (ou linha de uma tabela de verdade) atribui um valor de verdade ( T ou F ) a cada variável proposicional p . Então, os valores de verdade das orações complexas são calculados com tabelas de verdade. Na semântica modal, um conjunto W de mundos possíveis é introduzido. A valorização, em seguida, dá um valor de verdade para cada variável proposicional para cada um dos mundos possíveis em W . Isso significa que o valor atribuído a p para o mundo w pode diferir do valor atribuído a p para outro mundo w '.
O valor de verdade da sentença atômica p no mundo w dado pela avaliação v pode ser escrito v ( p, w ). Dada esta notação, os valores de verdade ( T para true, F for false) de orações complexas de lógica modal para uma avaliação dada v (e membro w do conjunto de mundos W ) podem ser definidos pelas seguintes cláusulas de verdade. ('iff' abreviado 'se e somente se'.)
(~) V (~ A , w ) = T sse v ( A , w ) = F .(→) v ( A → B , w ) = T sse v ( A , w ) = F ou v ( B , w ) = T .(5) v (□ A , w ) = T sse para cada mundo w 'em W , v ( A , W ') = t .
Cláusulas (~) e (→) simplesmente descrevem o comportamento padrão da tabela de verdade para negação e implicação material, respectivamente. De acordo com (5), □ A é verdadeira (em um mundo w ) exatamente quando A é verdade em todos os mundos possíveis. Dada a definição de ◊, (a saber, ◊ A = ~ □ ~ A ), a condição de verdade (5) assegura que ◊ A é verdade apenas no caso de A ser verdade em algum mundo possível. Uma vez que as cláusulas de verdade para □ e ◊ envolvem os quantificadores "todos" e "alguns" (respectivamente), serão esperados paralelos no comportamento lógico entre □ e ∀ x , e entre ◊ e ∃ x observados na seção 2.
Cláusulas (~), (→) e (5) permitem calcular o valor de verdade de qualquer frase em qualquer mundo em uma determinada avaliação. Uma definição de validade está agora ao virar da esquina. Um argumento é 5-válido para um determinado conjunto W (de mundos possíveis) se e somente se cada avaliação das orações atômicas que atribuem as premissas T em um mundo em W também atribui a conclusão T no mesmo mundo. Um argumento é dito ser 5 válido se for válido para todos os conjuntos não vazios W de mundos possíveis.
Foi mostrado que S5 é som e completo para validade 5 (daí o uso do símbolo '5'). Os argumentos válidos em 5 são exatamente os argumentos prováveis no S5 . Este resultado sugere que S5 é a maneira correta de formular uma lógica de necessidade.
No entanto, S5 não é uma lógica razoável para todos os membros da família modal. Na lógica deontica, lógica temporal e outros, o análogo da condição de verdade (5) claramente não é apropriado; Além disso, há mesmo concepções de necessidade onde (5) deve ser rejeitado também. O ponto é mais fácil de ver no caso da lógica temporal. Aqui, os membros de W são momentos de tempo, ou mundos "congelados", por assim dizer, em um instante. Para simplificar, vamos considerar um futuro lógica temporal, uma lógica onde □ A lê: 'ele vai ser sempre o caso que'. (Nós formulamos o sistema usando □ em vez do tradicional Gde modo que as conexões com outras lógicas modais sejam mais fáceis de apreciar.) A cláusula correta para □ deve dizer que □ A é verdadeira no tempo w se A é verdade em todo o tempo no futuro de w. Para restringir a atenção para o futuro, a relação R (para 'eRlier than') precisa ser introduzida. Então, a cláusula correta pode ser formulada da seguinte forma.
( K ) v (□ A , w ) = T sse para cada w ', se w R w ', em seguida, v ( A , W ') = t .
Isso diz que □ A é verdade em w , caso o A seja verdadeiro em todos os momentos depois de w .
A validade para esta marca de lógica temporal agora pode ser definida. Um quadro < W , R > é um par que consiste de um conjunto não vazio W (de mundos) e uma relação binária R em W . Um modelo < F , v > consiste de um quadro F , e uma valorização v que atribui valores de verdade para cada sentença atômica em cada mundo em W . Dado um modelo, os valores de todas as orações complexas podem ser determinados usando (~), (→) e ( K ). Um argumento é K- valido apenas no caso de qualquer modelo cuja avaliação atribua as premissas TEm um mundo também atribui a conclusão T no mesmo mundo. Como o leitor pode ter adivinhado com o uso de ' K ', demonstrou-se que a lógica modal mais simples K é som e completa para a validade K.
7. Axiomas e Condições Modais nos Quadros
Pode-se supor a partir desta discussão que K é a lógica correta quando □ é lido "sempre será o caso". No entanto, existem razões para pensar que K é muito fraco. Uma característica lógica óbvia da relação R (anterior) é a transitividade. Se w R v ( w for anterior a v ) e v R u ( v é anterior a você ), segue-se que w R u ( w é anterior a você ). Então, vamos definir um novo tipo de validade que corresponda a esta condição em R. Deixe um 4-modelo ser qualquer modelo cuja moldura < W , R > é tal que R é uma relação transitiva em W . Então, um argumento é válido em 4 se qualquer modelo de 4 cuja avaliação atribua T às instalações em um mundo também atribui T à conclusão no mesmo mundo. Usamos '4' para descrever um modelo tão transitivo porque a lógica adequada (som e completa) para 4 validades é K4 , a lógica que resulta da adição do axioma (4): □ A → □□ A a K .
A transitividade não é a única propriedade que podemos querer exigir do quadro < W , R > se Rdeve ser lido "antes do que" e W é um conjunto de momentos. Uma condição (que é apenas um pouco controverso) é que não há último instante de tempo, ou seja, que para cada mundo w há algum mundo v tal que w R v . Essa condição em quadros é chamada de serialidade. Serialidade corresponde ao axioma ( D ): □ A → ◊ A , da mesma forma que a transitividade corresponde a (4). Um modelo D é um K- modela com um quadro serial. A partir do conceito de modelo D, a noção correspondente de D -validez pode ser definida exatamente como fizemos no caso da validade 4. Como você provavelmente adivinhou, o sistema que é adequado em relação à D- validade é KD , ou K plus ( D ). Não só isso, mas o sistema KD4 (isto é K de adição (4) e ( D )) é adequado em relação à D4 -validity, onde um D4 -model é um onde < W , R > é tanto em série e transitória.
Outra propriedade que podemos querer para a relação "anterior a" é a densidade, a condição que diz que, entre duas vezes, sempre podemos encontrar outra. A densidade seria falsa se o tempo fosse atômico, ou seja, se houvesse intervalos de tempo que não pudessem ser divididos em partes menores. A densidade corresponde ao axioma ( C4 ): □□ A → □ A , o inverso de (4), por exemplo, o sistema KC4 , que é K plus ( C4 ) é adequado em relação aos modelos onde o quadro < W , R > é denso e KDC4 , adequado em relação aos modelos cujos quadros são seriais e densos, e assim por diante.
Cada um dos axiomas de lógica modal que discutimos corresponde a uma condição nos quadros da mesma maneira. A relação entre condições em quadros e axiomas correspondentes é um dos temas centrais no estudo de lógicas modais. Uma vez que uma interpretação do operador intensional □ foi decidida, as condições apropriadas em R podem ser determinadas para consertar a noção de validade correspondente. Isso, por sua vez, nos permite selecionar o conjunto certo de axiomas para essa lógica.
Por exemplo, considere uma lógica deontica, onde □ é lido "é obrigatório que". Aqui, a verdade de □ A não exige a verdade de A em todo mundo possível, mas apenas em um subconjunto daqueles mundos onde as pessoas fazem o que deveriam. Então, queremos apresentar uma relação R para este tipo de lógica e usar a cláusula de verdade ( K ) para avaliar □ A em um mundo. No entanto, neste caso, R não é anterior. Em vez disso, w R w 'detém apenas no caso de mundo w ' é uma variável moralmente aceitável de w, ou seja, um mundo que as nossas ações possam provocar que satisfaça o que é moralmente correto, ou certo, ou apenas. Sob essa leitura, deve ficar claro que os quadros relevantes devem obedecer a serialidade, a condição que exige que cada mundo possível tenha uma variável moralmente aceitável. A análise das propriedades desejadas para Rtorna claro que uma lógica deôntico básico pode ser formulado por adição de axioma ( D ) e para K .
Mesmo na lógica modal, pode-se desejar restringir a gama de mundos possíveis que sejam relevantes para determinar se □ A é verdade em um determinado mundo. Por exemplo, posso dizer que é necessário que eu pague minhas contas, mesmo sabendo muito bem que existe um mundo possível onde eu não as pague. No discurso comum, a afirmação de que A é necessária não requer a verdade de A em todos os mundos possíveis, mas sim apenas em uma certa classe de mundos que eu tenho em mente (por exemplo, mundos onde eu evito as penalidades por falta de pagamento) . A fim de proporcionar um tratamento genérico de necessidade, devemos dizer que □ Um é verdade em w sse A é verdadeiro em todos os mundosque estão relacionados com w no caminho certo. Assim, para um operador □ interpretado como necessidade, apresentamos uma relação R correspondente ao conjunto de possíveis mundos W , tradicionalmente denominado relação de acessibilidade. A relação de acessibilidade R é válida entre os mundos w e w 'iff w ' é possível, dado os fatos de w . Sob esta leitura para R , deve ficar claro que os quadros para a lógica modal devem ser reflexivos. Segue-se que a lógica modal deve ser fundada em M , o sistema resultante da adição ( M ) a K. Dependendo exatamente da forma como a relação de acessibilidade é entendida, simetria e transitividade também podem ser desejadas.
Uma lista de algumas das condições mais discutidas em quadros e seus axiomas correspondentes, juntamente com um mapa que mostra a relação entre as várias lógicas modais, podem ser encontradas na próxima seção.
Pode-se supor a partir desta discussão que K é a lógica correta quando □ é lido "sempre será o caso". No entanto, existem razões para pensar que K é muito fraco. Uma característica lógica óbvia da relação R (anterior) é a transitividade. Se w R v ( w for anterior a v ) e v R u ( v é anterior a você ), segue-se que w R u ( w é anterior a você ). Então, vamos definir um novo tipo de validade que corresponda a esta condição em R. Deixe um 4-modelo ser qualquer modelo cuja moldura < W , R > é tal que R é uma relação transitiva em W . Então, um argumento é válido em 4 se qualquer modelo de 4 cuja avaliação atribua T às instalações em um mundo também atribui T à conclusão no mesmo mundo. Usamos '4' para descrever um modelo tão transitivo porque a lógica adequada (som e completa) para 4 validades é K4 , a lógica que resulta da adição do axioma (4): □ A → □□ A a K .
A transitividade não é a única propriedade que podemos querer exigir do quadro < W , R > se Rdeve ser lido "antes do que" e W é um conjunto de momentos. Uma condição (que é apenas um pouco controverso) é que não há último instante de tempo, ou seja, que para cada mundo w há algum mundo v tal que w R v . Essa condição em quadros é chamada de serialidade. Serialidade corresponde ao axioma ( D ): □ A → ◊ A , da mesma forma que a transitividade corresponde a (4). Um modelo D é um K- modela com um quadro serial. A partir do conceito de modelo D, a noção correspondente de D -validez pode ser definida exatamente como fizemos no caso da validade 4. Como você provavelmente adivinhou, o sistema que é adequado em relação à D- validade é KD , ou K plus ( D ). Não só isso, mas o sistema KD4 (isto é K de adição (4) e ( D )) é adequado em relação à D4 -validity, onde um D4 -model é um onde < W , R > é tanto em série e transitória.
Outra propriedade que podemos querer para a relação "anterior a" é a densidade, a condição que diz que, entre duas vezes, sempre podemos encontrar outra. A densidade seria falsa se o tempo fosse atômico, ou seja, se houvesse intervalos de tempo que não pudessem ser divididos em partes menores. A densidade corresponde ao axioma ( C4 ): □□ A → □ A , o inverso de (4), por exemplo, o sistema KC4 , que é K plus ( C4 ) é adequado em relação aos modelos onde o quadro < W , R > é denso e KDC4 , adequado em relação aos modelos cujos quadros são seriais e densos, e assim por diante.
Cada um dos axiomas de lógica modal que discutimos corresponde a uma condição nos quadros da mesma maneira. A relação entre condições em quadros e axiomas correspondentes é um dos temas centrais no estudo de lógicas modais. Uma vez que uma interpretação do operador intensional □ foi decidida, as condições apropriadas em R podem ser determinadas para consertar a noção de validade correspondente. Isso, por sua vez, nos permite selecionar o conjunto certo de axiomas para essa lógica.
Por exemplo, considere uma lógica deontica, onde □ é lido "é obrigatório que". Aqui, a verdade de □ A não exige a verdade de A em todo mundo possível, mas apenas em um subconjunto daqueles mundos onde as pessoas fazem o que deveriam. Então, queremos apresentar uma relação R para este tipo de lógica e usar a cláusula de verdade ( K ) para avaliar □ A em um mundo. No entanto, neste caso, R não é anterior. Em vez disso, w R w 'detém apenas no caso de mundo w ' é uma variável moralmente aceitável de w, ou seja, um mundo que as nossas ações possam provocar que satisfaça o que é moralmente correto, ou certo, ou apenas. Sob essa leitura, deve ficar claro que os quadros relevantes devem obedecer a serialidade, a condição que exige que cada mundo possível tenha uma variável moralmente aceitável. A análise das propriedades desejadas para Rtorna claro que uma lógica deôntico básico pode ser formulado por adição de axioma ( D ) e para K .
Mesmo na lógica modal, pode-se desejar restringir a gama de mundos possíveis que sejam relevantes para determinar se □ A é verdade em um determinado mundo. Por exemplo, posso dizer que é necessário que eu pague minhas contas, mesmo sabendo muito bem que existe um mundo possível onde eu não as pague. No discurso comum, a afirmação de que A é necessária não requer a verdade de A em todos os mundos possíveis, mas sim apenas em uma certa classe de mundos que eu tenho em mente (por exemplo, mundos onde eu evito as penalidades por falta de pagamento) . A fim de proporcionar um tratamento genérico de necessidade, devemos dizer que □ Um é verdade em w sse A é verdadeiro em todos os mundosque estão relacionados com w no caminho certo. Assim, para um operador □ interpretado como necessidade, apresentamos uma relação R correspondente ao conjunto de possíveis mundos W , tradicionalmente denominado relação de acessibilidade. A relação de acessibilidade R é válida entre os mundos w e w 'iff w ' é possível, dado os fatos de w . Sob esta leitura para R , deve ficar claro que os quadros para a lógica modal devem ser reflexivos. Segue-se que a lógica modal deve ser fundada em M , o sistema resultante da adição ( M ) a K. Dependendo exatamente da forma como a relação de acessibilidade é entendida, simetria e transitividade também podem ser desejadas.
Uma lista de algumas das condições mais discutidas em quadros e seus axiomas correspondentes, juntamente com um mapa que mostra a relação entre as várias lógicas modais, podem ser encontradas na próxima seção.
8. Mapa das Relações entre Logs Modais
O diagrama a seguir mostra as relações entre as lógicas modais melhor conhecidos, nomeadamente lógicas que podem ser formados por adição de uma selecção dos axiomas ( D ), ( M ), (4), ( B ) e (5) a K . Uma lista desses (e outros) axiomas, juntamente com suas condições de quadro correspondentes, pode ser encontrada abaixo do diagrama.
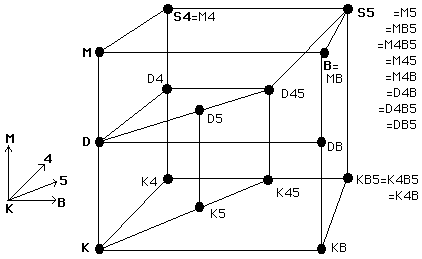
Neste gráfico, os sistemas são fornecidos pela lista de seus axiomas. Assim, por exemplo M4B é o resultado da adição de ( H ), (4) e ( B ) para K . Em negrito, indicamos nomes tradicionais de alguns sistemas. Quando o sistema S é exibido abaixo e / ou para a esquerda de S 'ligadas por uma linha, em seguida, S ' é uma extensão de S . Isto significa que todos os argumentos demonstrável em S é demonstrável em S ', mas S é mais fraco do que S ', ou seja, não todos os argumentos demonstráveis em S 'são demonstráveis em S .
A lista a seguir indica axiomas, seus nomes e as condições correspondentes na relação de acessibilidade R , para axiomas até agora discutidos nesta entrada de enciclopédia.
Nome do axiomaAxioma Condição em quadros R é ... ( D ) □ A → ◊ A ∃ u w R u Serial ( M ) □ A → A w R w Reflexivo (4) □ A → □□ A ( w R v & v R u ) ⇒ w R u Transitivo ( B ) A → □ ◊ A w R v ⇒ v R w Simétrico (5) ◊ A → □ ◊ A ( w R v & w R u ) ⇒ v R u Euclidiana ( C D ) ◊ A → □ A ( w R v & w R u ) ⇒ v = u Funcional (□ M ) □ (□ A → A ) w R v ⇒ v R v Shift
Reflexive ( C4 ) □□ A → □ A w R v ⇒ ∃ u ( w R u & u R v ) Denso ( C ) ◊ □ A → □ ◊ A w R v & w R x ⇒ ∃ u ( v R u & x R u ) Convergente
Na lista de condições em quadros, e no resto deste artigo, as variáveis ' w ', ' v ', ' u ', ' x ' e o quantificador '∃ u ' são entendidos como variam ao longo W . '&' abreviado 'e' e '⇒ abre abreviação' se ... então '.
A noção de correspondência entre axiomas e condições de quadro que está em questão aqui foi explicada na seção anterior. Quando S é uma lista de axiomas e F (S) é o conjunto correspondente de condições de quadro, então S corresponde a F (S) exatamente quando o sistema K + S é adequado (som e completo) para validade F (S) Ou seja, um argumento é provável em K + S se for F (S) -valid. Várias noções mais fortes de correspondência entre axiomas e condições de quadros surgiram na pesquisa sobre lógica modal.
O diagrama a seguir mostra as relações entre as lógicas modais melhor conhecidos, nomeadamente lógicas que podem ser formados por adição de uma selecção dos axiomas ( D ), ( M ), (4), ( B ) e (5) a K . Uma lista desses (e outros) axiomas, juntamente com suas condições de quadro correspondentes, pode ser encontrada abaixo do diagrama.
Neste gráfico, os sistemas são fornecidos pela lista de seus axiomas. Assim, por exemplo M4B é o resultado da adição de ( H ), (4) e ( B ) para K . Em negrito, indicamos nomes tradicionais de alguns sistemas. Quando o sistema S é exibido abaixo e / ou para a esquerda de S 'ligadas por uma linha, em seguida, S ' é uma extensão de S . Isto significa que todos os argumentos demonstrável em S é demonstrável em S ', mas S é mais fraco do que S ', ou seja, não todos os argumentos demonstráveis em S 'são demonstráveis em S .
A lista a seguir indica axiomas, seus nomes e as condições correspondentes na relação de acessibilidade R , para axiomas até agora discutidos nesta entrada de enciclopédia.
Nome do axioma | Axioma | Condição em quadros | R é ... |
| ( D ) | □ A → ◊ A | ∃ u w R u | Serial |
| ( M ) | □ A → A | w R w | Reflexivo |
| (4) | □ A → □□ A | ( w R v & v R u ) ⇒ w R u | Transitivo |
| ( B ) | A → □ ◊ A | w R v ⇒ v R w | Simétrico |
| (5) | ◊ A → □ ◊ A | ( w R v & w R u ) ⇒ v R u | Euclidiana |
| ( C D ) | ◊ A → □ A | ( w R v & w R u ) ⇒ v = u | Funcional |
| (□ M ) | □ (□ A → A ) | w R v ⇒ v R v | Shift Reflexive |
| ( C4 ) | □□ A → □ A | w R v ⇒ ∃ u ( w R u & u R v ) | Denso |
| ( C ) | ◊ □ A → □ ◊ A | w R v & w R x ⇒ ∃ u ( v R u & x R u ) | Convergente |
Na lista de condições em quadros, e no resto deste artigo, as variáveis ' w ', ' v ', ' u ', ' x ' e o quantificador '∃ u ' são entendidos como variam ao longo W . '&' abreviado 'e' e '⇒ abre abreviação' se ... então '.
A noção de correspondência entre axiomas e condições de quadro que está em questão aqui foi explicada na seção anterior. Quando S é uma lista de axiomas e F (S) é o conjunto correspondente de condições de quadro, então S corresponde a F (S) exatamente quando o sistema K + S é adequado (som e completo) para validade F (S) Ou seja, um argumento é provável em K + S se for F (S) -valid. Várias noções mais fortes de correspondência entre axiomas e condições de quadros surgiram na pesquisa sobre lógica modal.
9. O Axioma Geral
A correspondência entre axiomas e condições nos quadros pode parecer algo de um mistério. Um resultado bonito de Lemmon e Scott (1977) vai um longo caminho para explicar esses relacionamentos. O seu teorema diz respeito aos axiomas que têm a seguinte forma:
( G ) ◊ h □ i A → □ j ◊ k A
Usamos a notação '◊ n ' para representar n diamantes em uma linha, então, por exemplo, '◊ 3 ' abreviam uma série de três diamantes: '◊◊◊'. Da mesma forma, "□ n " representa uma série decaixas n . Quando os valores de h , i , j e k são todos 1, temos axioma ( C ):
( C ) ◊ □ A → □ ◊ A = ◊ 1 □ 1 A → □ 1 ◊ 1 A
O axioma ( B ) resulta da configuração h e i para 0 e deixando j e k ser 1:
( B ) A → □ ◊ A = ◊ 0 □ 0 A → □ 1 ◊ 1 A
Para obter (4), podemos definir h e k para 0, definir i para 1 e j para 2:
(4) □ A → □□ A = ◊ 0 □ 1 A → □ 2 ◊ 0 A
Muitos (mas não todos) axiomas de lógica modal podem ser obtidos definindo os valores corretos para os parâmetros em ( G )
Nossa próxima tarefa será dar a condição em quadros que correspondem a ( G ) para uma determinada seleção de valores para h , i , j e k . Para isso, precisaremos de uma definição. A composição de duas relações R e R 'é uma nova relação R 
R ' que é definida da seguinte forma:
w R R ' v iff for some u , w R u e u R ' v .
Por exemplo, se R é a relação de ser um irmão, e R 'é a relação de ser um pai então R R ' é a relação de ser um tio, (porque w é o tio de v sse para alguns pessoa u , tanto w é o irmão de vocêe você é o pai de v ). Uma relação pode ser composta por si mesma. Por exemplo, quando R é a relação de ser pai, então R R é a relação de ser avô e R R R é a relação de ser um bisavô. Será útil escrever ' R n ', pelo resultado de compor R com ele mesmo n vezes. Então, R 2 é R R , e R 4é R R R R . Vamos deixar R 1 ser R , e R 0 será a relação de identidade, ou seja, w R 0 v iff w = v .
Podemos agora indicar o resultado de Scott-Lemmon. É que a condição em quadros que corresponde exatamente a qualquer axioma da forma ( G ) é a seguinte.
( h i j k -Convergência) w R h v & w R j u ⇒ ∃ x ( v R i x & u R k x )
É interessante ver como as condições familiares em R resultam da configuração dos valores para h , i , j e k de acordo com os valores no axioma correspondente. Por exemplo, considere (5). Nesse caso, i = 0 e h = j = k = 1. Portanto, a condição correspondente é
w R v & w R u ⇒ ∃ x ( v R 0 x & u R x ).
Explicamos que R 0 é a relação de identidade. Então, se v R 0 x então v = x . Mas ∃ x ( v = x & u R x ), é equivalente a u R v , e assim a condição euclidiana é obtida:
( w R v & w R u ) ⇒ u R v .
No caso do axioma (4), h = 0, i = 1, j = 2 e k = 0. Portanto, a condição correspondente em quadros é
( w = v & w R 2 u ) ⇒ ∃ x ( v R x & u = x ).
Resolvendo as identidades, isso equivale a:
v R 2 u ⇒ v R u .
Pela definição de R 2 , v R 2 u iff ∃ x ( v R x & x R u ), então isso vem para:
∃ x ( v R x & x R u ) ⇒ v R u ,
que por lógica de predicado, é equivalente à transitividade.
v R x & x R u ⇒ v R u .
O leitor pode achar um exercício agradável para ver como as condições correspondentes caem da hijk-Convergence quando os valores dos parâmetros h , i , j e k são definidos por outros axiomas.
Os resultados de Scott-Lemmon fornecem um método rápido para estabelecer resultados sobre a relação entre axiomas e suas condições de quadro correspondentes. Uma vez que mostraram a adequação de qualquer lógica que estenda K com uma seleção de axiomas da forma ( G ) em relação a modelos que satisfaçam o conjunto correspondente de condições de quadros, eles forneceram provas de adequação "grossistas" para a maioria dos sistemas no modal família. Sahlqvist (1975) descobriu generalizações importantes do resultado de Scott-Lemmon cobrindo uma gama muito maior de tipos de axioma.
O leitor deve ser advertido, no entanto, de que a correspondência perfeita entre axiomas e condições nos quadros é atípica. Há configurações em quadros que não correspondem a nenhum axioma, e há condições uniformes em quadros para os quais nenhum sistema é adequado. (Para um exemplo, veja Boolos, 1993, pp. 148ff.)
A correspondência entre axiomas e condições nos quadros pode parecer algo de um mistério. Um resultado bonito de Lemmon e Scott (1977) vai um longo caminho para explicar esses relacionamentos. O seu teorema diz respeito aos axiomas que têm a seguinte forma:
( G ) ◊ h □ i A → □ j ◊ k A
Usamos a notação '◊ n ' para representar n diamantes em uma linha, então, por exemplo, '◊ 3 ' abreviam uma série de três diamantes: '◊◊◊'. Da mesma forma, "□ n " representa uma série decaixas n . Quando os valores de h , i , j e k são todos 1, temos axioma ( C ):
( C ) ◊ □ A → □ ◊ A = ◊ 1 □ 1 A → □ 1 ◊ 1 A
O axioma ( B ) resulta da configuração h e i para 0 e deixando j e k ser 1:
( B ) A → □ ◊ A = ◊ 0 □ 0 A → □ 1 ◊ 1 A
Para obter (4), podemos definir h e k para 0, definir i para 1 e j para 2:
(4) □ A → □□ A = ◊ 0 □ 1 A → □ 2 ◊ 0 A
Muitos (mas não todos) axiomas de lógica modal podem ser obtidos definindo os valores corretos para os parâmetros em ( G )
Nossa próxima tarefa será dar a condição em quadros que correspondem a ( G ) para uma determinada seleção de valores para h , i , j e k . Para isso, precisaremos de uma definição. A composição de duas relações R e R 'é uma nova relação R R ' que é definida da seguinte forma:
R ' que é definida da seguinte forma:w R
Por exemplo, se R é a relação de ser um irmão, e R 'é a relação de ser um pai então R R ' é a relação de ser um tio, (porque w é o tio de v sse para alguns pessoa u , tanto w é o irmão de vocêe você é o pai de v ). Uma relação pode ser composta por si mesma. Por exemplo, quando R é a relação de ser pai, então R R é a relação de ser avô e R R R é a relação de ser um bisavô. Será útil escrever ' R n ', pelo resultado de compor R com ele mesmo n vezes. Então, R 2 é R R , e R 4é R R R R . Vamos deixar R 1 ser R , e R 0 será a relação de identidade, ou seja, w R 0 v iff w = v .
R ' é a relação de ser um tio, (porque w é o tio de v sse para alguns pessoa u , tanto w é o irmão de vocêe você é o pai de v ). Uma relação pode ser composta por si mesma. Por exemplo, quando R é a relação de ser pai, então R R é a relação de ser avô e R R R é a relação de ser um bisavô. Será útil escrever ' R n ', pelo resultado de compor R com ele mesmo n vezes. Então, R 2 é R R , e R 4é R R R R . Vamos deixar R 1 ser R , e R 0 será a relação de identidade, ou seja, w R 0 v iff w = v .
Podemos agora indicar o resultado de Scott-Lemmon. É que a condição em quadros que corresponde exatamente a qualquer axioma da forma ( G ) é a seguinte.
( h i j k -Convergência) w R h v & w R j u ⇒ ∃ x ( v R i x & u R k x )
É interessante ver como as condições familiares em R resultam da configuração dos valores para h , i , j e k de acordo com os valores no axioma correspondente. Por exemplo, considere (5). Nesse caso, i = 0 e h = j = k = 1. Portanto, a condição correspondente é
w R v & w R u ⇒ ∃ x ( v R 0 x & u R x ).
Explicamos que R 0 é a relação de identidade. Então, se v R 0 x então v = x . Mas ∃ x ( v = x & u R x ), é equivalente a u R v , e assim a condição euclidiana é obtida:
( w R v & w R u ) ⇒ u R v .
No caso do axioma (4), h = 0, i = 1, j = 2 e k = 0. Portanto, a condição correspondente em quadros é
( w = v & w R 2 u ) ⇒ ∃ x ( v R x & u = x ).
Resolvendo as identidades, isso equivale a:
v R 2 u ⇒ v R u .
Pela definição de R 2 , v R 2 u iff ∃ x ( v R x & x R u ), então isso vem para:
∃ x ( v R x & x R u ) ⇒ v R u ,
que por lógica de predicado, é equivalente à transitividade.
v R x & x R u ⇒ v R u .
O leitor pode achar um exercício agradável para ver como as condições correspondentes caem da hijk-Convergence quando os valores dos parâmetros h , i , j e k são definidos por outros axiomas.
Os resultados de Scott-Lemmon fornecem um método rápido para estabelecer resultados sobre a relação entre axiomas e suas condições de quadro correspondentes. Uma vez que mostraram a adequação de qualquer lógica que estenda K com uma seleção de axiomas da forma ( G ) em relação a modelos que satisfaçam o conjunto correspondente de condições de quadros, eles forneceram provas de adequação "grossistas" para a maioria dos sistemas no modal família. Sahlqvist (1975) descobriu generalizações importantes do resultado de Scott-Lemmon cobrindo uma gama muito maior de tipos de axioma.
O leitor deve ser advertido, no entanto, de que a correspondência perfeita entre axiomas e condições nos quadros é atípica. Há configurações em quadros que não correspondem a nenhum axioma, e há condições uniformes em quadros para os quais nenhum sistema é adequado. (Para um exemplo, veja Boolos, 1993, pp. 148ff.)
10. Semântica bidimensional
A semântica bidimensional é uma variante da possível semântica mundial que usa dois (ou mais) tipos de parâmetros na avaliação da verdade, em vez de possíveis mundos sozinhos. Por exemplo, uma lógica de expressões indexadas, como "I", "aqui", "agora", e similares, precisa trazer o contexto lingüístico (ou contexto curto). Dado um contexto c = < s , p , t > onde s é o alto-falante, p o local e t o tempo de pronúncia, então 'I' se refere a s , 'aqui' para p , e 'agora' para t . Então, no contexto c = <Jim Garson, Houston, 3:00 PM CST em 3/3/2014> "Estou aqui agora" é T iff Jim Garson está em Houston, às 3:00 da tarde, CST, em 3/3/2014.
Em possíveis semânticas mundiais, o valor de verdade de uma frase dependia do mundo em que é avaliado. No entanto, os índices trazem uma segunda dimensão - então precisamos generalizar novamente. Kaplan (1989) define o caracter de uma sentença B como uma função do conjunto de contextos (linguísticos) para o conteúdo (ou intensão) de B, onde o conteúdo, por sua vez, é simplesmente a intensão de B, isto é, um Funcionar de mundos possíveis para valores de verdade. Aqui, a avaliação da verdade é duplamente dependente - tanto em contextos linguísticos quanto em possíveis mundos.
Uma das observações mais interessantes de Kaplan é que algumas frases indexais são contingentes, mas, ao mesmo tempo, são analiticamente verdadeiras. Um exemplo é (1).
(1) Estou aqui agora.
Apenas pelo significado das palavras, você pode ver que (1) deve ser verdade em qualquer contexto c = < s , p , t >. Afinal, c conta como um contexto lingüístico no caso de s é um falante que está no lugar p no tempo t . Portanto (1) é verdadeiro em c, e isso significa que o padrão de valores de verdade (1) tem ao longo da dimensão de contexto deve ser todo Ts (dado o mundo possível é mantido fixo). Isso sugere que a dimensão do contexto é apta para rastrear o conhecimento analítico obtido a partir do domínio da nossa linguagem. Por outro lado, a dimensão dos mundos possíveis acompanha o que é necessário. Mantendo o contexto fixo, existem mundos possíveis onde (1) é falso. Por exemplo, quando c = <Jim Garson, Houston, 3:00 PM CST em 3/3/2014>, (1) falha em c em um mundo possível onde Jim Garson está em Boston às 3:00 da tarde CST em 4 / 3/2014. Segue-se que "eu estou aqui agora" é uma verdade analítica contingente. Portanto, a semântica bidimensional pode lidar com situações em que a necessidade e a analítica se separam.
Outro exemplo em que se traz duas dimensões é útil na lógica de um futuro aberto (Thomason, 1984; Belnap, et al., 2001). Aqui, emprega uma estrutura temporal onde muitas possíveis histórias futuras se estendem a partir de um determinado momento. Considere (2).
(2) Joe ordenará uma batalha no mar amanhã.
Se (2) é contingente, então existe um possível histórico em que a batalha ocorre no dia seguinte ao da avaliação e outra onde não ocorre então. Então, para avaliar (2) você precisa saber duas coisas: qual é o tempo t de avaliação e qual das histórias h que correm através de t é a que deve ser considerada. Portanto, uma frase dessa lógica é avaliada em um par < t , h >.
Outro problema resolvido pela semântica bidimensional é a interação entre "agora" e outras expressões temporais como o tempo futuro "será o caso". Então, é plausível pensar que "agora" se refere ao tempo de avaliação. Então, teríamos a seguinte condição de verdade:
(Agora) v (Agora B , t ) = T iff v ( B , t ) = T.
No entanto, isso não funcionará para frases como (3).
(3) Em algum momento do futuro, todos os que vivem agora serão desconhecidos.
Com F como operador do tempo futuro, (3) pode ser traduzido:
(3) 'F∀ x (Agora Lx → Ux ).
(A tradução correta não pode ser ∀ x (Agora Lx → F Ux ), com F tendo um escopo estreito, porque (3) diz que há um tempo futuro em que todas as coisas agora vivas são desconhecidas, não que cada ser vivo seja desconhecido em algum tempo futuro próprio). Quando as condições de verdade para (3) 'calculado, usando (Agora) e a condição de verdade (F) para F, verifica-se que (3)' é verdadeiro no momento u se houver um tempo t depois de você de modo que tudo o que está vivendo em t (não você !) é desconhecido em t .
(F) v (F B , t ) = T iff por algum tempo u mais tarde do que t , v ( B , u ) = T.
Para avaliar (3) 'corretamente para que ele corresponda ao que queremos dizer (3), devemos ter certeza de que' agora 'sempre se remete ao tempo original de pronúncia quando' agora 'está no âmbito de outros operadores temporais, como F. Portanto, precisamos acompanhar o tempo que é a hora da pronúncia ( u ), bem como qual é o tempo de avaliação ( t ). Então, nossos índices assumem a forma de um par < u , e >, onde você é o momento da pronunciação, e e é o momento da avaliação. Então a condição de verdade (Agora) é revisada para (2DNow).
(2DNow) v (Agora B , < u , e >) = T iff v ( B , < u , u >) = T.
Isso tem que o Now B é verdadeiro em um momento de pronúncia e tempo de avaliação, desde que B seja verdade quando você é considerado o momento da avaliação. Quando as condições de verdade para F, ∀ e → são revisadas da maneira óbvia (basta ignorar o u no par), (3) 'é verdadeiro em < u , e > desde que exista um tempo e ' posterior a e de modo que tudo o que está vivendo em você é desconhecido em e '. Ao levar um registro do que você é durante o cálculo da verdade, sempre podemos corrigir o valor de "agora" para o tempo original de emissão, mesmo quando "agora" está profundamente incorporado em outros operadores temporais.
Aparece um fenômeno semelhante nas lógicas modais com um operador de atuação A (leia "na verdade, é o caso"). Para avaliar adequadamente (4), precisamos acompanhar o mundo que é considerado o mundo real (ou real), bem como o que é levado ao mundo da avaliação.
(4) É possível que todos os seres vivos sejam desconhecidos.
A idéia de distinguir as diferentes dimensões mundiais possíveis na semântica teve aplicações úteis na filosofia. Por exemplo, Chalmers (1996) apresentou argumentos a partir da concepção de (dizer) zumbis para conclusões dualistas na filosofia da mente. Chalmers (2006) implantou semântica bidimensional para ajudar a identificar um aspecto a priori do significado que apoiaria tais conclusões.
A idéia também foi implantada na filosofia da linguagem. Kripke (1980) argumentou que 'Water is H2O' é uma posteriori, mas, no entanto, uma verdade necessária, pois, dado que a água é apenas H20, não existe um mundo possível em que essa coisa seja (digamos) um elemento básico como os gregos achavam. Por outro lado, há uma forte intuição de que o mundo real foi algo diferente do que é, o líquido inodoro que cai do céu como a chuva, enche nossos lagos e rios, etc. poderia perfeitamente ter sido um elemento. Então, em algum sentido, é concebível que a água não seja H20. A semântica bidimensional abre espaço para essas intuições, fornecendo uma dimensão separada que rastreia uma concepção de água que deixa de lado a natureza química do que a água realmente é.
A semântica bidimensional é uma variante da possível semântica mundial que usa dois (ou mais) tipos de parâmetros na avaliação da verdade, em vez de possíveis mundos sozinhos. Por exemplo, uma lógica de expressões indexadas, como "I", "aqui", "agora", e similares, precisa trazer o contexto lingüístico (ou contexto curto). Dado um contexto c = < s , p , t > onde s é o alto-falante, p o local e t o tempo de pronúncia, então 'I' se refere a s , 'aqui' para p , e 'agora' para t . Então, no contexto c = <Jim Garson, Houston, 3:00 PM CST em 3/3/2014> "Estou aqui agora" é T iff Jim Garson está em Houston, às 3:00 da tarde, CST, em 3/3/2014.
Em possíveis semânticas mundiais, o valor de verdade de uma frase dependia do mundo em que é avaliado. No entanto, os índices trazem uma segunda dimensão - então precisamos generalizar novamente. Kaplan (1989) define o caracter de uma sentença B como uma função do conjunto de contextos (linguísticos) para o conteúdo (ou intensão) de B, onde o conteúdo, por sua vez, é simplesmente a intensão de B, isto é, um Funcionar de mundos possíveis para valores de verdade. Aqui, a avaliação da verdade é duplamente dependente - tanto em contextos linguísticos quanto em possíveis mundos.
Uma das observações mais interessantes de Kaplan é que algumas frases indexais são contingentes, mas, ao mesmo tempo, são analiticamente verdadeiras. Um exemplo é (1).
(1) Estou aqui agora.
Apenas pelo significado das palavras, você pode ver que (1) deve ser verdade em qualquer contexto c = < s , p , t >. Afinal, c conta como um contexto lingüístico no caso de s é um falante que está no lugar p no tempo t . Portanto (1) é verdadeiro em c, e isso significa que o padrão de valores de verdade (1) tem ao longo da dimensão de contexto deve ser todo Ts (dado o mundo possível é mantido fixo). Isso sugere que a dimensão do contexto é apta para rastrear o conhecimento analítico obtido a partir do domínio da nossa linguagem. Por outro lado, a dimensão dos mundos possíveis acompanha o que é necessário. Mantendo o contexto fixo, existem mundos possíveis onde (1) é falso. Por exemplo, quando c = <Jim Garson, Houston, 3:00 PM CST em 3/3/2014>, (1) falha em c em um mundo possível onde Jim Garson está em Boston às 3:00 da tarde CST em 4 / 3/2014. Segue-se que "eu estou aqui agora" é uma verdade analítica contingente. Portanto, a semântica bidimensional pode lidar com situações em que a necessidade e a analítica se separam.
Outro exemplo em que se traz duas dimensões é útil na lógica de um futuro aberto (Thomason, 1984; Belnap, et al., 2001). Aqui, emprega uma estrutura temporal onde muitas possíveis histórias futuras se estendem a partir de um determinado momento. Considere (2).
(2) Joe ordenará uma batalha no mar amanhã.
Se (2) é contingente, então existe um possível histórico em que a batalha ocorre no dia seguinte ao da avaliação e outra onde não ocorre então. Então, para avaliar (2) você precisa saber duas coisas: qual é o tempo t de avaliação e qual das histórias h que correm através de t é a que deve ser considerada. Portanto, uma frase dessa lógica é avaliada em um par < t , h >.
Outro problema resolvido pela semântica bidimensional é a interação entre "agora" e outras expressões temporais como o tempo futuro "será o caso". Então, é plausível pensar que "agora" se refere ao tempo de avaliação. Então, teríamos a seguinte condição de verdade:
(Agora) v (Agora B , t ) = T iff v ( B , t ) = T.
No entanto, isso não funcionará para frases como (3).
(3) Em algum momento do futuro, todos os que vivem agora serão desconhecidos.
Com F como operador do tempo futuro, (3) pode ser traduzido:
(3) 'F∀ x (Agora Lx → Ux ).
(A tradução correta não pode ser ∀ x (Agora Lx → F Ux ), com F tendo um escopo estreito, porque (3) diz que há um tempo futuro em que todas as coisas agora vivas são desconhecidas, não que cada ser vivo seja desconhecido em algum tempo futuro próprio). Quando as condições de verdade para (3) 'calculado, usando (Agora) e a condição de verdade (F) para F, verifica-se que (3)' é verdadeiro no momento u se houver um tempo t depois de você de modo que tudo o que está vivendo em t (não você !) é desconhecido em t .
(F) v (F B , t ) = T iff por algum tempo u mais tarde do que t , v ( B , u ) = T.
Para avaliar (3) 'corretamente para que ele corresponda ao que queremos dizer (3), devemos ter certeza de que' agora 'sempre se remete ao tempo original de pronúncia quando' agora 'está no âmbito de outros operadores temporais, como F. Portanto, precisamos acompanhar o tempo que é a hora da pronúncia ( u ), bem como qual é o tempo de avaliação ( t ). Então, nossos índices assumem a forma de um par < u , e >, onde você é o momento da pronunciação, e e é o momento da avaliação. Então a condição de verdade (Agora) é revisada para (2DNow).
(2DNow) v (Agora B , < u , e >) = T iff v ( B , < u , u >) = T.
Isso tem que o Now B é verdadeiro em um momento de pronúncia e tempo de avaliação, desde que B seja verdade quando você é considerado o momento da avaliação. Quando as condições de verdade para F, ∀ e → são revisadas da maneira óbvia (basta ignorar o u no par), (3) 'é verdadeiro em < u , e > desde que exista um tempo e ' posterior a e de modo que tudo o que está vivendo em você é desconhecido em e '. Ao levar um registro do que você é durante o cálculo da verdade, sempre podemos corrigir o valor de "agora" para o tempo original de emissão, mesmo quando "agora" está profundamente incorporado em outros operadores temporais.
Aparece um fenômeno semelhante nas lógicas modais com um operador de atuação A (leia "na verdade, é o caso"). Para avaliar adequadamente (4), precisamos acompanhar o mundo que é considerado o mundo real (ou real), bem como o que é levado ao mundo da avaliação.
(4) É possível que todos os seres vivos sejam desconhecidos.
A idéia de distinguir as diferentes dimensões mundiais possíveis na semântica teve aplicações úteis na filosofia. Por exemplo, Chalmers (1996) apresentou argumentos a partir da concepção de (dizer) zumbis para conclusões dualistas na filosofia da mente. Chalmers (2006) implantou semântica bidimensional para ajudar a identificar um aspecto a priori do significado que apoiaria tais conclusões.
A idéia também foi implantada na filosofia da linguagem. Kripke (1980) argumentou que 'Water is H2O' é uma posteriori, mas, no entanto, uma verdade necessária, pois, dado que a água é apenas H20, não existe um mundo possível em que essa coisa seja (digamos) um elemento básico como os gregos achavam. Por outro lado, há uma forte intuição de que o mundo real foi algo diferente do que é, o líquido inodoro que cai do céu como a chuva, enche nossos lagos e rios, etc. poderia perfeitamente ter sido um elemento. Então, em algum sentido, é concebível que a água não seja H20. A semântica bidimensional abre espaço para essas intuições, fornecendo uma dimensão separada que rastreia uma concepção de água que deixa de lado a natureza química do que a água realmente é.
11. Logística de provabilidade
A lógica modal tem sido útil para esclarecer nossa compreensão dos resultados centrais referentes à provabilidade nos fundamentos da matemática (Boolos, 1993). As lógicas de provabilidade são sistemas em que as variáveis proposicionais p , q , r , etc. variam em fórmulas de algum sistema matemático, por exemplo o sistema PA de Peano para aritmética. (O sistema escolhido para matemática pode variar, mas assume que é PA para essa discussão.) Gödel mostrou que a aritmética possui fortes poderes expressivos. Usando números de código para frases aritméticas, ele foi capaz de demonstrar uma correspondência entre frases de matemática e fatos sobre quais frases são e não são prováveis em PA. Por exemplo, ele mostrou que há uma sentença C que é verdade apenas no caso de nenhuma contradição ser provável em PA e há uma sentença G (a famosa sentença de Gödel) que é verdade apenas no caso de não ser provável na PA.
Na lógica de provabilidade, □ p é interpretado como uma fórmula (de aritmética) que expressa que o que p denota é provável na PA . Usando esta notação, frases de lógica de provabilidade expressam fatos sobre provabilidade. Suponha que ⊥ seja uma lógica constante de provabilidade que denota uma contradição. Então ~ □ ⊥ diz que PA é consistente e □ A → A diz que PA é som no sentido de que, quando prova A , A é verdade. Além disso, a caixa pode ser iterada. Então, por exemplo, □ ~ □ ⊥ faz a duvidosa afirmação de que PA é capaz de provar sua própria consistência, e ~ □ ⊥ → ~ □ ~ □ ⊥ afirma (corretamente como Gödel provou) que, se PA é consistente, a PAnão pode comprovar sua própria consistência.
Embora as lógicas de provabilidade formem uma família de sistemas relacionados, o sistema GLé, de longe, o mais conhecido. Isso resulta da adição do seguinte axioma a K :
( GL ) □ (□ A → A ) → □ A
O axioma (4): □ A → □□ A é provável em GL , então GL é realmente um fortalecimento de K4 . No entanto, axiomas como ( M ): □ A → A , e até os mais fracos ( D ): □ A → ◊ A não estão disponíveis (nem desejáveis) em GL . Na lógica de provabilidade, a provabilidade não deve ser tratada como uma marca de necessidade. A razão é que, quando p é provável em um sistema arbitrário S para matemática, não se segue que p é verdade, uma vez que S pode ser insuficiente. Além disso, se p é provável em S (□ p ) que nem precisa seguir que ~ p não possui uma prova (~ □ ~ p = ◊ p ). S pode ser inconsistente e assim provar ambos p e ~ p .
Axioma ( GL ) captura o conteúdo do Teorema de Loeb, um resultado importante nos fundamentos da aritmética. □ A → A diz que PA é som para A , ou seja, se A foi comprovada, A seria verdadeira. (Essa afirmação pode não ser segura para um sistema S arbitrariamente selecionado , uma vez que A pode ser provável em S e falso.) ( GL ) alega que, se PA conseguir provar a sentença que reivindica solidez para uma determinada frase A , então A é já provável na PA . Teorema de Loeb relata um tipo de modéstia na PAparte de (Boolos, 1993, p. 55). PA não insiste (prova) de que uma prova de A implica A verdade 's, a menos que já tem uma prova de Apara sustentar essa afirmação.
Foi demonstrado que o GL é adequado para a provabilidade no sentido a seguir. Deixe uma frase de GL ser sempre provável exatamente quando a sentença de aritmética que ele indica é provável, não importa como suas variáveis são atribuídas valores a frases de PA . Então as frases prováveis de GL são exatamente as frases que são sempre prováveis. Este resultado de adequação tem sido extremamente útil, uma vez que as questões gerais relativas à provabilidade na PApodem ser transformadas em questões mais fáceis sobre o que pode ser demonstrado no GL .
GL também pode ser equipado com uma possível semântica mundial para a qual é som e completo. Uma condição correspondente em quadros para GL- validity é que o quadro seja transitivo, finito e irreflexivo.
A lógica modal tem sido útil para esclarecer nossa compreensão dos resultados centrais referentes à provabilidade nos fundamentos da matemática (Boolos, 1993). As lógicas de provabilidade são sistemas em que as variáveis proposicionais p , q , r , etc. variam em fórmulas de algum sistema matemático, por exemplo o sistema PA de Peano para aritmética. (O sistema escolhido para matemática pode variar, mas assume que é PA para essa discussão.) Gödel mostrou que a aritmética possui fortes poderes expressivos. Usando números de código para frases aritméticas, ele foi capaz de demonstrar uma correspondência entre frases de matemática e fatos sobre quais frases são e não são prováveis em PA. Por exemplo, ele mostrou que há uma sentença C que é verdade apenas no caso de nenhuma contradição ser provável em PA e há uma sentença G (a famosa sentença de Gödel) que é verdade apenas no caso de não ser provável na PA.
Na lógica de provabilidade, □ p é interpretado como uma fórmula (de aritmética) que expressa que o que p denota é provável na PA . Usando esta notação, frases de lógica de provabilidade expressam fatos sobre provabilidade. Suponha que ⊥ seja uma lógica constante de provabilidade que denota uma contradição. Então ~ □ ⊥ diz que PA é consistente e □ A → A diz que PA é som no sentido de que, quando prova A , A é verdade. Além disso, a caixa pode ser iterada. Então, por exemplo, □ ~ □ ⊥ faz a duvidosa afirmação de que PA é capaz de provar sua própria consistência, e ~ □ ⊥ → ~ □ ~ □ ⊥ afirma (corretamente como Gödel provou) que, se PA é consistente, a PAnão pode comprovar sua própria consistência.
Embora as lógicas de provabilidade formem uma família de sistemas relacionados, o sistema GLé, de longe, o mais conhecido. Isso resulta da adição do seguinte axioma a K :
( GL ) □ (□ A → A ) → □ A
O axioma (4): □ A → □□ A é provável em GL , então GL é realmente um fortalecimento de K4 . No entanto, axiomas como ( M ): □ A → A , e até os mais fracos ( D ): □ A → ◊ A não estão disponíveis (nem desejáveis) em GL . Na lógica de provabilidade, a provabilidade não deve ser tratada como uma marca de necessidade. A razão é que, quando p é provável em um sistema arbitrário S para matemática, não se segue que p é verdade, uma vez que S pode ser insuficiente. Além disso, se p é provável em S (□ p ) que nem precisa seguir que ~ p não possui uma prova (~ □ ~ p = ◊ p ). S pode ser inconsistente e assim provar ambos p e ~ p .
Axioma ( GL ) captura o conteúdo do Teorema de Loeb, um resultado importante nos fundamentos da aritmética. □ A → A diz que PA é som para A , ou seja, se A foi comprovada, A seria verdadeira. (Essa afirmação pode não ser segura para um sistema S arbitrariamente selecionado , uma vez que A pode ser provável em S e falso.) ( GL ) alega que, se PA conseguir provar a sentença que reivindica solidez para uma determinada frase A , então A é já provável na PA . Teorema de Loeb relata um tipo de modéstia na PAparte de (Boolos, 1993, p. 55). PA não insiste (prova) de que uma prova de A implica A verdade 's, a menos que já tem uma prova de Apara sustentar essa afirmação.
Foi demonstrado que o GL é adequado para a provabilidade no sentido a seguir. Deixe uma frase de GL ser sempre provável exatamente quando a sentença de aritmética que ele indica é provável, não importa como suas variáveis são atribuídas valores a frases de PA . Então as frases prováveis de GL são exatamente as frases que são sempre prováveis. Este resultado de adequação tem sido extremamente útil, uma vez que as questões gerais relativas à provabilidade na PApodem ser transformadas em questões mais fáceis sobre o que pode ser demonstrado no GL .
GL também pode ser equipado com uma possível semântica mundial para a qual é som e completo. Uma condição correspondente em quadros para GL- validity é que o quadro seja transitivo, finito e irreflexivo.
12. Lógica Modal Avançada
As aplicações da lógica modal para matemática e ciência da computação tornaram-se cada vez mais importantes. A lógica de provabilidade é apenas um exemplo dessa tendência. O termo "lógica modal avançada" refere-se a uma tradição na pesquisa de lógica modal que é particularmente bem representada nos departamentos de matemática e informática. Esta tradição foi tecida na história da lógica modal desde seus primórdios (Goldblatt, 2006). A pesquisa em relacionamentos com topologia e álgebras representa alguns dos primeiros trabalhos técnicos sobre lógica modal. No entanto, o termo "lógica modal avançada" geralmente se refere a uma segunda onda de trabalho realizado desde meados da década de 1970.
As aplicações da lógica modal para matemática e ciência da computação tornaram-se cada vez mais importantes. A lógica de provabilidade é apenas um exemplo dessa tendência. O termo "lógica modal avançada" refere-se a uma tradição na pesquisa de lógica modal que é particularmente bem representada nos departamentos de matemática e informática. Esta tradição foi tecida na história da lógica modal desde seus primórdios (Goldblatt, 2006). A pesquisa em relacionamentos com topologia e álgebras representa alguns dos primeiros trabalhos técnicos sobre lógica modal. No entanto, o termo "lógica modal avançada" geralmente se refere a uma segunda onda de trabalho realizado desde meados da década de 1970.
13. Bisimulação
Bisimulação fornece um bom exemplo das interações frutíferas que foram desenvolvidas entre lógica modal e ciência da computação. Em ciência da computação, sistemas de transição rotulados (LTSs) são comumente usados para representar possíveis caminhos de computação durante a execução de um programa. As LTSs são generalizações de quadros Kripke, consistindo em um conjunto W de estados e uma coleção de i - relações de acessibilidade R i , uma para cada processo de computador i . Intuitivamente, w R i w 'contém exatamente quando w ' é um estado que resulta da aplicação do processo i ao estado w .
A linguagem da lógica monodimensional ou dinâmica introduz uma coleção de operadores modais □ i , uma para cada programa i (Harel, 1984). Então □ i A afirma que a sentença A é válida em cada resultado de aplicação de i . Assim, idéias como a exatidão e a conclusão bem sucedida dos programas podem ser expressas neste idioma. Os modelos para tal linguagem são como modelos Kripke, salvo que os LTSs sejam usados no lugar dos quadros. Uma bisimulação é uma relação de contrapartida entre estados de dois desses modelos, de modo que exatamente as mesmas variáveis proposicionais são verdadeiras em estados de contraparte e sempre que mundov é eu-acessível de um dos dois estados de contrapartida, então a outra contrapartida tem a relação de acessibilidade i para alguma contrapartida de v . Em suma, a estrutura de i-acessibilidade que um pode "ver" de um determinado estado imita o que se vê de uma contraparte. A bisimulação é uma noção mais fraca do que o isomorfismo (uma relação de bisimulação não precisa ser 1-1), mas é suficiente para garantir a equivalência no processamento.
Na década de 1970, uma versão de bisimulação já havia sido desenvolvida por logis modal para ajudar a compreender melhor a relação entre axiomas de lógica modal e suas condições correspondentes em quadros Kripke. Semântica de Kripke fornece uma base para a tradução axiomas modais em frases de uma linguagem de segunda ordem, onde a quantificação é permitido mais de um local de cartas de predicados P . Substitua as metavariáveis A por orações abertas P x, traduzem □ P x para ∀ y ( R x y → P y ) e feche as variáveis livres x e letras predicadas Pcom quantificadores universais. Por exemplo, a tradução da lógica do predicado do esquema do axioma □ A → A vem para ∀ P ∀ x [∀ y ( R x y → P y ) → P x ]. Dada esta tradução, pode-se instanciar a variável P para um predicado arbitrário de um lugar, por exemplo, para o predicado Rxcuja extensão é o conjunto de todos os mundos w, tal que Rxw para um determinado valor de x . Então, obtém ∀ x [∀ y ( R x y →R x y ) → R x x ], que se reduz a ∀ x R x x , uma vez que ∀ y ( R x y → R x y ) é uma tautologia. Isso ilumina a correspondência entre □ A → A e reflexividade de quadros (∀ x R x x). Resultados semelhantes são válidos para muitos outros axiomas e condições de quadros. O "colapso" de condições de axioma de segunda ordem para condições de quadro de primeira ordem é muito útil na obtenção de resultados completos para lógicas modais. Por exemplo, esta é a idéia central por trás dos resultados elegantes de Sahlqvist (1975).
Mas quando a tradução de um axioma de segunda ordem reduz a condição de primeira ordem em Rnesse caminho? Na década de 1970, van Benthem mostrou que isso acontece se a tradição em um modelo implica a sua participação em qualquer modelo bisimular, onde dois modelos são bisimulares se houver uma bisimulação entre eles no caso especial, onde existe uma relação de acessibilidade única. Esse resultado generaliza facilmente o caso poli-modal (van Benthem 1996, p. 88). Isso sugere que a lógica policromática está exatamente no nível certo de abstração para descrever, e a razão, a computação e outros processos. (Afinal, o que realmente interessa é a preservação dos valores de verdade das fórmulas nos modelos, em vez dos detalhes mais finos das estruturas do quadro.) Além disso, a tradução implícita dessas lógicas em fragmentos bem entendidos da lógica do predicado fornece uma riqueza de informações de interesse para cientistas da computação. Como um resultado,et al. 1995).
Bisimulação fornece um bom exemplo das interações frutíferas que foram desenvolvidas entre lógica modal e ciência da computação. Em ciência da computação, sistemas de transição rotulados (LTSs) são comumente usados para representar possíveis caminhos de computação durante a execução de um programa. As LTSs são generalizações de quadros Kripke, consistindo em um conjunto W de estados e uma coleção de i - relações de acessibilidade R i , uma para cada processo de computador i . Intuitivamente, w R i w 'contém exatamente quando w ' é um estado que resulta da aplicação do processo i ao estado w .
A linguagem da lógica monodimensional ou dinâmica introduz uma coleção de operadores modais □ i , uma para cada programa i (Harel, 1984). Então □ i A afirma que a sentença A é válida em cada resultado de aplicação de i . Assim, idéias como a exatidão e a conclusão bem sucedida dos programas podem ser expressas neste idioma. Os modelos para tal linguagem são como modelos Kripke, salvo que os LTSs sejam usados no lugar dos quadros. Uma bisimulação é uma relação de contrapartida entre estados de dois desses modelos, de modo que exatamente as mesmas variáveis proposicionais são verdadeiras em estados de contraparte e sempre que mundov é eu-acessível de um dos dois estados de contrapartida, então a outra contrapartida tem a relação de acessibilidade i para alguma contrapartida de v . Em suma, a estrutura de i-acessibilidade que um pode "ver" de um determinado estado imita o que se vê de uma contraparte. A bisimulação é uma noção mais fraca do que o isomorfismo (uma relação de bisimulação não precisa ser 1-1), mas é suficiente para garantir a equivalência no processamento.
Na década de 1970, uma versão de bisimulação já havia sido desenvolvida por logis modal para ajudar a compreender melhor a relação entre axiomas de lógica modal e suas condições correspondentes em quadros Kripke. Semântica de Kripke fornece uma base para a tradução axiomas modais em frases de uma linguagem de segunda ordem, onde a quantificação é permitido mais de um local de cartas de predicados P . Substitua as metavariáveis A por orações abertas P x, traduzem □ P x para ∀ y ( R x y → P y ) e feche as variáveis livres x e letras predicadas Pcom quantificadores universais. Por exemplo, a tradução da lógica do predicado do esquema do axioma □ A → A vem para ∀ P ∀ x [∀ y ( R x y → P y ) → P x ]. Dada esta tradução, pode-se instanciar a variável P para um predicado arbitrário de um lugar, por exemplo, para o predicado Rxcuja extensão é o conjunto de todos os mundos w, tal que Rxw para um determinado valor de x . Então, obtém ∀ x [∀ y ( R x y →R x y ) → R x x ], que se reduz a ∀ x R x x , uma vez que ∀ y ( R x y → R x y ) é uma tautologia. Isso ilumina a correspondência entre □ A → A e reflexividade de quadros (∀ x R x x). Resultados semelhantes são válidos para muitos outros axiomas e condições de quadros. O "colapso" de condições de axioma de segunda ordem para condições de quadro de primeira ordem é muito útil na obtenção de resultados completos para lógicas modais. Por exemplo, esta é a idéia central por trás dos resultados elegantes de Sahlqvist (1975).
Mas quando a tradução de um axioma de segunda ordem reduz a condição de primeira ordem em Rnesse caminho? Na década de 1970, van Benthem mostrou que isso acontece se a tradição em um modelo implica a sua participação em qualquer modelo bisimular, onde dois modelos são bisimulares se houver uma bisimulação entre eles no caso especial, onde existe uma relação de acessibilidade única. Esse resultado generaliza facilmente o caso poli-modal (van Benthem 1996, p. 88). Isso sugere que a lógica policromática está exatamente no nível certo de abstração para descrever, e a razão, a computação e outros processos. (Afinal, o que realmente interessa é a preservação dos valores de verdade das fórmulas nos modelos, em vez dos detalhes mais finos das estruturas do quadro.) Além disso, a tradução implícita dessas lógicas em fragmentos bem entendidos da lógica do predicado fornece uma riqueza de informações de interesse para cientistas da computação. Como um resultado,et al. 1995).
14. Quantificadores na lógica modal
Parece ser uma questão simples equiparar uma lógica modal com os quantificadores ∀ (todos) e ∃ (alguns). Simplesmente adicionaria as regras padrão (ou clássicas) para quantificadores aos princípios de qualquer lógica modal proposicional que se escolha. No entanto, adicionar quantificadores à lógica modal envolve várias dificuldades. Alguns são filosóficos. Por exemplo, Quine (1953) argumentou que a quantificação em contextos modais é simplesmente incoerente, uma visão que gerou uma literatura gigantesca. As queixas de Quine não carregam o peso que uma vez fizeram. (Veja Barcan 1990 para um bom resumo.) No entanto, a visão de que há algo de errado com "quantificar in" ainda é amplamente realizada. Um segundo tipo de complicação é técnico. Existe uma ampla variedade nas escolhas que pode ser feita na semântica para a lógica modal quantificada, e a prova de que um sistema de regras é correto para uma determinada escolha pode ser difícil. O trabalho de Corsi (2002) e Garson (2005) contribui de alguma forma para a união deste terreno, mas a situação continua a ser desafiadora.
Outra complicação é que alguns lógicos acreditam que essa modalidade requer o abandono das regras de quantificação clássicas em favor das regras mais fracas da lógica livre (Garson, 2001). Os principais pontos de desacordo sobre as regras de quantificação podem ser rastreados em decisões sobre como lidar com o domínio de quantificação. A alternativa mais simples, a abordagem de domínio fixo (às vezes chamado de possibilista), assume um único domínio de quantificação que contém todos os objetos possíveis. Por outro lado, a interpretação relativa ao mundo (ou realista), pressupõe que o domínio da quantificação muda de mundo para mundo e contém apenas os objetos que realmente existem em um determinado mundo.
A abordagem de domínio fixo não requer grandes ajustes na maquinaria clássica para os quantificadores. As lógicas modais que são adequadas para a semântica de domínio fixo geralmente podem ser axiomatizadas pela adição de princípios de uma lógica modal proposicional às regras clássicas de quantificação junto com a Fórmula Barcan ( B F ) (Barcan 1946). (Para uma conta de algumas exceções interessantes, veja Cresswell (1995)).
( B F ) ∀ x □ Um → □ ∀ x Uma .
A interpretação de domínio fixo possui vantagens de simplicidade e familiaridade, mas não fornece uma descrição direta da semântica de certas expressões quantificadoras de linguagem natural. Nós não pensamos que "algum homem existe que assinou a Declaração de Independência" é verdade, pelo menos não, se lemos "existe" no tempo presente. No entanto, esta sentença foi verdadeira em 1777, o que mostra que o domínio para a expressão da linguagem natural "existe algum homem" que muda para refletir quais homens existem em momentos diferentes. Um problema relacionado é aquele na interpretação de domínio fixo, a sentença ∀ y □ ∃ x ( x = y ) é válida. Supondo que ∃ x ( x = y ) seja lido:y existe, ∀ y □ ∃ x ( x = y ) diz que tudo existe necessariamente. No entanto, parece uma característica fundamental de idéias comuns sobre a modalidade de que a existência de muitas coisas é contingente e que existem diferentes objetos em diferentes mundos possíveis.
O defensor da interpretação de domínio fixo pode responder a essas objeções insistindo que, na leitura dos quantificadores, o domínio da quantificação contém todos os objetos possíveis, não apenas os objetos que existem em um determinado mundo. Assim, o teorema ∀ y □ ∃ x ( x = y ) faz a afirmação inócua de que todo objeto possível é necessariamente encontrado no domínio de todos os objetos possíveis. Além disso, as expressões quantificadoras de linguagem natural cujo domínio é dependente do mundo (ou tempo) podem ser expressas usando o quantificador de domínio fixo ∃ x e uma letra de predicado Ecom a leitura "realmente existe". Por exemplo, ao invés de traduzir "Alguns M existe, que S Igned a Declaração de Independência" por
∃ x ( M x & S x ),
o defensor de domínios fixos pode escrever:
∃ x ( E x & M x & S x ),
garantindo assim que a tradução seja contada falso no momento. Cresswell (1991) faz a observação interessante de que a quantificação relativa do mundo tem um poder expressivo limitado em relação à quantificação de domínio fixo. A quantificação relativa do mundo pode ser definida com quantificadores de domínio fixos e E , mas não há maneira de expressar completamente os quantificadores de domínio fixo com os relacionados ao mundo. Embora isso defenda a abordagem clássica da lógica modal quantificada, a tática de tradução também equivale a uma concessão em favor da lógica livre, pois os quantificadores relativos ao mundo assim definidos obedecem exatamente às regras da lógica livre.
Um problema com a estratégia de tradução utilizada pelos defensores da quantificação fixa de domínio é que tornar o inglês em lógica é menos direto, já que E deve ser adicionado a todas as traduções de todas as frases cujas expressões quantificadoras têm domínios dependentes do contexto. Uma objeção mais séria à quantificação de domínio fixo é que ele tira o quantificador de um papel que a Quine recomendou para ele, ou seja, registrar um compromisso ontológico robusto. Nesta visão, o domínio de ∃ x deve conter apenas entidades que são ontologicamente respeitáveis, e os objetos possíveis são muito abstratos para se qualificar. Os atuais desta faixa querem desenvolver a lógica de um quantificador ∃ x que reflete o compromisso com o que é real em um determinado mundo e não com o que é meramente possível.
No entanto, trabalhos recentes sobre o atualismo tende a minar essa objeção. Por exemplo, Linsky e Zalta (1994) argumentam que o quantificador de domínio fixo pode receber uma interpretação perfeitamente aceitável para os realistas. Os realistas que empregam a semântica dos mundos possíveis rotineiramente quantificam sobre possíveis mundos em sua teoria semântica da linguagem. Assim, parece que os mundos possíveis são reais pelas luzes desses realistas. Ao habilmente equipar o domínio com entidades abstratas não mais censuráveis do que as que os realistas aceitam, Linsky e Zalta mostram que a fórmula Barcan e os princípios clássicos podem ser vindicados. Note, no entanto, que os realistas podem responder que não precisam estar comprometidos com a realidade dos possíveis mundos, desde que se entenda que os quantificadores usados em sua teoria da linguagem não possuem uma forte importação ontológica. Em qualquer caso, é aberto a realistas (e não realistas também) para investigar a lógica de quantificadores com domínios mais robustos, por exemplo, domínios que excluam mundos possíveis e outras entidades abstratas, e que contém apenas os detalhes espaciotemporais encontrados em um determinado mundo. Para os quantificadores deste tipo, um domínio relativo ao mundo é apropriado.
Tais considerações motivam o interesse em sistemas que reconhecem a dependência do contexto de quantificação através da introdução de domínios mundiais. Aqui, cada mundo possível tem seu próprio domínio de quantificação (o conjunto de objetos que realmente existem nesse mundo), e os domínios variam de um mundo para o outro. Quando esta decisão é tomada, surge uma dificuldade para a teoria da quantificação clássica. Observe que a frase ∃ x ( x = t ) é um teorema da lógica clássica, e assim □ ∃ x ( x = t ) é um teorema de K pela Regra de Necessidade. Deixe o termo t representam Saul Kripke. Então este teorema diz que é necessário que Saul Kripke exista, para que ele esteja no domínio de todo mundo possível. Toda a motivação para a abordagem relativa ao mundo era refletir a idéia de que os objetos em um mundo podem não existir em outro. Se os governantes quantificadores padrão forem usados, no entanto, cada termo t deve se referir a algo que existe em todos os mundos possíveis. Isso parece incompatível com nossa prática comum de usar termos para se referir a coisas que só existem contingentemente.
Uma resposta a esta dificuldade é simplesmente eliminar termos. Kripke (1963) dá um exemplo de um sistema que usa a interpretação relativa ao mundo e preserva as regras clássicas. No entanto, os custos são graves. Primeiro, sua linguagem é artificialmente empobrecida, e segundo, as regras para a lógica modal proposicional devem ser enfraquecidas.
Presumindo que gostaríamos de um idioma que inclua termos e que as regras clássicas sejam adicionadas a sistemas padrão de lógica modal proposicional, surge um novo problema. Em tal sistema, é possível provar ( C B F ), o inverso da Fórmula Barcan.
( C B F ) □ ∀ x Um → ∀ x □ Uma .
Esse fato tem sérias conseqüências para a semântica do sistema. Não é difícil mostrar que cada modelo relativo ao mundo de ( C B F ) deve atender à condição ( N D ) (para "domínios aninhados").
( N D ) Se w R v então o domínio de w é um subconjunto do domínio de v .
No entanto ( N D ) conflita com o ponto de introduzir domínios relativos ao mundo. Toda a idéia era que a existência de objetos é contingente para que haja possíveis mundos possíveis onde uma das coisas em nosso mundo não existe.
Uma solução direta para esses problemas é abandonar as regras clássicas para os quantificadores e adotar regras para a lógica livre ( FL ). As regras de FL são as mesmas que as regras clássicas, exceto que as inferências de ∀ x R x (tudo é real) para R p (Pegasus é real) são bloqueadas. Isso é feito introduzindo um predicado ' E ' (para 'realmente existe') e modificando a regra da instanciação universal. De ∀ x R x um é permitido obter R p somente se um também obteve E p . Supondo que o quantificador universal ∀ xé primitivo e o quantificador existencial ∃ x é definido por ∃ x A = df ~ ∀ x ~ A , então FL pode ser construído adicionando os seguintes dois princípios às regras da lógica proposicional
Generalização universal. Se B → ( E y → A ( y )) é um teorema, assim é B → ∀ x A ( x ).
Instantiation Universal. ∀ x A ( x ) → ( E n → A ( n ))
(Aqui é assumido que A ( x ) é qualquer fórmula bem formada de lógica de predicado, e que A ( y) e A ( n ) resultam da substituição de y e n adequadamente para cada ocorrência de x em A ( x ).) Note-se que o axioma de instanciação é restrito por menção de En no antecedente. A regra da generalização universal é modificada da mesma maneira. Em FL , provas de fórmulas como ∃ x □ ( x = t ), ∀ y □ ∃ x (x = y ), ( C B F ) e ( B F ), que parecem incompatíveis com a interpretação relativa ao mundo, são bloqueados.
Uma objeção filosófica para FL é que E parece ser um predicado de existência, e muitos argumentariam que a existência não é uma propriedade legítima como ser verde ou pesando mais de quatro libras. Portanto, os filósofos que rejeitam a idéia de que a existência é um predicado podem se opor à FL . No entanto, na maioria (mas não em todas) lógicas modais quantificadas que incluem identidade (=), essas preocupações podem ser contornadas definindo E como segue.
E t = df ∃ x ( x = t ).
A maneira mais geral para formular lógica modal quantificada é criar FS adicionando as regras do FL a um determinado proposicional lógica modal S . Em situações onde a quantificação clássica é desejada, pode-se simplesmente adicionar E t como axioma a FS , de modo que os princípios clássicos se tornem regras deriváveis. Os resultados de adequação para tais sistemas podem ser obtidos para a maioria das escolhas da lógica modal S , mas existem exceções.
É digna de mencionar uma complicação final na semântica para a lógica modal quantificada. Ocorre quando expressões não-rígidas, como 'o inventor de bifocais', são introduzidas na linguagem. Um termo não é rígido quando escolhe objetos diferentes em diferentes mundos possíveis. O valor semântico de tal termo pode ser dado pelo que Carnap (1947) chamou de conceito individual, uma função que escolhe a denotação do termo para cada mundo possível. Uma abordagem para lidar com termos não rígidos é empregar a teoria das descrições de Russell. No entanto, em uma linguagem que trata expressões não rígidas como termos genuínos, verifica-se que nem as regras clássicas nem as de lógica livre para os quantificadores são aceitáveis. (O problema não pode ser resolvido enfraquecendo a regra de substituição pela identidade. ) Uma solução para este problema é empregar um tratamento mais geral dos quantificadores, onde o domínio de quantificação contém conceitos individuais em vez de objetos. Esta interpretação mais geral proporciona uma melhor combinação entre o tratamento de termos e o tratamento de quantificadores e resultados em sistemas adequados para regras lógicas clássicas ou livres (dependendo se os domínios fixos ou os domínios mundiais são escolhidos). Ele também fornece uma linguagem com potências expressivas fortes e muito necessárias (Bressan, 1973, Belnap e Müller, 2013a, 2013b), Esta interpretação mais geral proporciona uma melhor combinação entre o tratamento de termos e o tratamento de quantificadores e resultados em sistemas adequados para regras lógicas clássicas ou livres (dependendo se os domínios fixos ou os domínios mundiais são escolhidos). Ele também fornece uma linguagem com potências expressivas fortes e muito necessárias (Bressan, 1973, Belnap e Müller, 2013a, 2013b), Esta interpretação mais geral proporciona uma melhor combinação entre o tratamento de termos e o tratamento de quantificadores e resultados em sistemas adequados para regras lógicas clássicas ou livres (dependendo se os domínios fixos ou os domínios mundiais são escolhidos). Ele também fornece uma linguagem com potências expressivas fortes e muito necessárias (Bressan, 1973, Belnap e Müller, 2013a, 2013b),
Parece ser uma questão simples equiparar uma lógica modal com os quantificadores ∀ (todos) e ∃ (alguns). Simplesmente adicionaria as regras padrão (ou clássicas) para quantificadores aos princípios de qualquer lógica modal proposicional que se escolha. No entanto, adicionar quantificadores à lógica modal envolve várias dificuldades. Alguns são filosóficos. Por exemplo, Quine (1953) argumentou que a quantificação em contextos modais é simplesmente incoerente, uma visão que gerou uma literatura gigantesca. As queixas de Quine não carregam o peso que uma vez fizeram. (Veja Barcan 1990 para um bom resumo.) No entanto, a visão de que há algo de errado com "quantificar in" ainda é amplamente realizada. Um segundo tipo de complicação é técnico. Existe uma ampla variedade nas escolhas que pode ser feita na semântica para a lógica modal quantificada, e a prova de que um sistema de regras é correto para uma determinada escolha pode ser difícil. O trabalho de Corsi (2002) e Garson (2005) contribui de alguma forma para a união deste terreno, mas a situação continua a ser desafiadora.
Outra complicação é que alguns lógicos acreditam que essa modalidade requer o abandono das regras de quantificação clássicas em favor das regras mais fracas da lógica livre (Garson, 2001). Os principais pontos de desacordo sobre as regras de quantificação podem ser rastreados em decisões sobre como lidar com o domínio de quantificação. A alternativa mais simples, a abordagem de domínio fixo (às vezes chamado de possibilista), assume um único domínio de quantificação que contém todos os objetos possíveis. Por outro lado, a interpretação relativa ao mundo (ou realista), pressupõe que o domínio da quantificação muda de mundo para mundo e contém apenas os objetos que realmente existem em um determinado mundo.
A abordagem de domínio fixo não requer grandes ajustes na maquinaria clássica para os quantificadores. As lógicas modais que são adequadas para a semântica de domínio fixo geralmente podem ser axiomatizadas pela adição de princípios de uma lógica modal proposicional às regras clássicas de quantificação junto com a Fórmula Barcan ( B F ) (Barcan 1946). (Para uma conta de algumas exceções interessantes, veja Cresswell (1995)).
( B F ) ∀ x □ Um → □ ∀ x Uma .
A interpretação de domínio fixo possui vantagens de simplicidade e familiaridade, mas não fornece uma descrição direta da semântica de certas expressões quantificadoras de linguagem natural. Nós não pensamos que "algum homem existe que assinou a Declaração de Independência" é verdade, pelo menos não, se lemos "existe" no tempo presente. No entanto, esta sentença foi verdadeira em 1777, o que mostra que o domínio para a expressão da linguagem natural "existe algum homem" que muda para refletir quais homens existem em momentos diferentes. Um problema relacionado é aquele na interpretação de domínio fixo, a sentença ∀ y □ ∃ x ( x = y ) é válida. Supondo que ∃ x ( x = y ) seja lido:y existe, ∀ y □ ∃ x ( x = y ) diz que tudo existe necessariamente. No entanto, parece uma característica fundamental de idéias comuns sobre a modalidade de que a existência de muitas coisas é contingente e que existem diferentes objetos em diferentes mundos possíveis.
O defensor da interpretação de domínio fixo pode responder a essas objeções insistindo que, na leitura dos quantificadores, o domínio da quantificação contém todos os objetos possíveis, não apenas os objetos que existem em um determinado mundo. Assim, o teorema ∀ y □ ∃ x ( x = y ) faz a afirmação inócua de que todo objeto possível é necessariamente encontrado no domínio de todos os objetos possíveis. Além disso, as expressões quantificadoras de linguagem natural cujo domínio é dependente do mundo (ou tempo) podem ser expressas usando o quantificador de domínio fixo ∃ x e uma letra de predicado Ecom a leitura "realmente existe". Por exemplo, ao invés de traduzir "Alguns M existe, que S Igned a Declaração de Independência" por
∃ x ( M x & S x ),
o defensor de domínios fixos pode escrever:
∃ x ( E x & M x & S x ),
garantindo assim que a tradução seja contada falso no momento. Cresswell (1991) faz a observação interessante de que a quantificação relativa do mundo tem um poder expressivo limitado em relação à quantificação de domínio fixo. A quantificação relativa do mundo pode ser definida com quantificadores de domínio fixos e E , mas não há maneira de expressar completamente os quantificadores de domínio fixo com os relacionados ao mundo. Embora isso defenda a abordagem clássica da lógica modal quantificada, a tática de tradução também equivale a uma concessão em favor da lógica livre, pois os quantificadores relativos ao mundo assim definidos obedecem exatamente às regras da lógica livre.
Um problema com a estratégia de tradução utilizada pelos defensores da quantificação fixa de domínio é que tornar o inglês em lógica é menos direto, já que E deve ser adicionado a todas as traduções de todas as frases cujas expressões quantificadoras têm domínios dependentes do contexto. Uma objeção mais séria à quantificação de domínio fixo é que ele tira o quantificador de um papel que a Quine recomendou para ele, ou seja, registrar um compromisso ontológico robusto. Nesta visão, o domínio de ∃ x deve conter apenas entidades que são ontologicamente respeitáveis, e os objetos possíveis são muito abstratos para se qualificar. Os atuais desta faixa querem desenvolver a lógica de um quantificador ∃ x que reflete o compromisso com o que é real em um determinado mundo e não com o que é meramente possível.
No entanto, trabalhos recentes sobre o atualismo tende a minar essa objeção. Por exemplo, Linsky e Zalta (1994) argumentam que o quantificador de domínio fixo pode receber uma interpretação perfeitamente aceitável para os realistas. Os realistas que empregam a semântica dos mundos possíveis rotineiramente quantificam sobre possíveis mundos em sua teoria semântica da linguagem. Assim, parece que os mundos possíveis são reais pelas luzes desses realistas. Ao habilmente equipar o domínio com entidades abstratas não mais censuráveis do que as que os realistas aceitam, Linsky e Zalta mostram que a fórmula Barcan e os princípios clássicos podem ser vindicados. Note, no entanto, que os realistas podem responder que não precisam estar comprometidos com a realidade dos possíveis mundos, desde que se entenda que os quantificadores usados em sua teoria da linguagem não possuem uma forte importação ontológica. Em qualquer caso, é aberto a realistas (e não realistas também) para investigar a lógica de quantificadores com domínios mais robustos, por exemplo, domínios que excluam mundos possíveis e outras entidades abstratas, e que contém apenas os detalhes espaciotemporais encontrados em um determinado mundo. Para os quantificadores deste tipo, um domínio relativo ao mundo é apropriado.
Tais considerações motivam o interesse em sistemas que reconhecem a dependência do contexto de quantificação através da introdução de domínios mundiais. Aqui, cada mundo possível tem seu próprio domínio de quantificação (o conjunto de objetos que realmente existem nesse mundo), e os domínios variam de um mundo para o outro. Quando esta decisão é tomada, surge uma dificuldade para a teoria da quantificação clássica. Observe que a frase ∃ x ( x = t ) é um teorema da lógica clássica, e assim □ ∃ x ( x = t ) é um teorema de K pela Regra de Necessidade. Deixe o termo t representam Saul Kripke. Então este teorema diz que é necessário que Saul Kripke exista, para que ele esteja no domínio de todo mundo possível. Toda a motivação para a abordagem relativa ao mundo era refletir a idéia de que os objetos em um mundo podem não existir em outro. Se os governantes quantificadores padrão forem usados, no entanto, cada termo t deve se referir a algo que existe em todos os mundos possíveis. Isso parece incompatível com nossa prática comum de usar termos para se referir a coisas que só existem contingentemente.
Uma resposta a esta dificuldade é simplesmente eliminar termos. Kripke (1963) dá um exemplo de um sistema que usa a interpretação relativa ao mundo e preserva as regras clássicas. No entanto, os custos são graves. Primeiro, sua linguagem é artificialmente empobrecida, e segundo, as regras para a lógica modal proposicional devem ser enfraquecidas.
Presumindo que gostaríamos de um idioma que inclua termos e que as regras clássicas sejam adicionadas a sistemas padrão de lógica modal proposicional, surge um novo problema. Em tal sistema, é possível provar ( C B F ), o inverso da Fórmula Barcan.
( C B F ) □ ∀ x Um → ∀ x □ Uma .
Esse fato tem sérias conseqüências para a semântica do sistema. Não é difícil mostrar que cada modelo relativo ao mundo de ( C B F ) deve atender à condição ( N D ) (para "domínios aninhados").
( N D ) Se w R v então o domínio de w é um subconjunto do domínio de v .
No entanto ( N D ) conflita com o ponto de introduzir domínios relativos ao mundo. Toda a idéia era que a existência de objetos é contingente para que haja possíveis mundos possíveis onde uma das coisas em nosso mundo não existe.
Uma solução direta para esses problemas é abandonar as regras clássicas para os quantificadores e adotar regras para a lógica livre ( FL ). As regras de FL são as mesmas que as regras clássicas, exceto que as inferências de ∀ x R x (tudo é real) para R p (Pegasus é real) são bloqueadas. Isso é feito introduzindo um predicado ' E ' (para 'realmente existe') e modificando a regra da instanciação universal. De ∀ x R x um é permitido obter R p somente se um também obteve E p . Supondo que o quantificador universal ∀ xé primitivo e o quantificador existencial ∃ x é definido por ∃ x A = df ~ ∀ x ~ A , então FL pode ser construído adicionando os seguintes dois princípios às regras da lógica proposicional
Generalização universal. Se B → ( E y → A ( y )) é um teorema, assim é B → ∀ x A ( x ).Instantiation Universal. ∀ x A ( x ) → ( E n → A ( n ))
(Aqui é assumido que A ( x ) é qualquer fórmula bem formada de lógica de predicado, e que A ( y) e A ( n ) resultam da substituição de y e n adequadamente para cada ocorrência de x em A ( x ).) Note-se que o axioma de instanciação é restrito por menção de En no antecedente. A regra da generalização universal é modificada da mesma maneira. Em FL , provas de fórmulas como ∃ x □ ( x = t ), ∀ y □ ∃ x (x = y ), ( C B F ) e ( B F ), que parecem incompatíveis com a interpretação relativa ao mundo, são bloqueados.
Uma objeção filosófica para FL é que E parece ser um predicado de existência, e muitos argumentariam que a existência não é uma propriedade legítima como ser verde ou pesando mais de quatro libras. Portanto, os filósofos que rejeitam a idéia de que a existência é um predicado podem se opor à FL . No entanto, na maioria (mas não em todas) lógicas modais quantificadas que incluem identidade (=), essas preocupações podem ser contornadas definindo E como segue.
E t = df ∃ x ( x = t ).
A maneira mais geral para formular lógica modal quantificada é criar FS adicionando as regras do FL a um determinado proposicional lógica modal S . Em situações onde a quantificação clássica é desejada, pode-se simplesmente adicionar E t como axioma a FS , de modo que os princípios clássicos se tornem regras deriváveis. Os resultados de adequação para tais sistemas podem ser obtidos para a maioria das escolhas da lógica modal S , mas existem exceções.
É digna de mencionar uma complicação final na semântica para a lógica modal quantificada. Ocorre quando expressões não-rígidas, como 'o inventor de bifocais', são introduzidas na linguagem. Um termo não é rígido quando escolhe objetos diferentes em diferentes mundos possíveis. O valor semântico de tal termo pode ser dado pelo que Carnap (1947) chamou de conceito individual, uma função que escolhe a denotação do termo para cada mundo possível. Uma abordagem para lidar com termos não rígidos é empregar a teoria das descrições de Russell. No entanto, em uma linguagem que trata expressões não rígidas como termos genuínos, verifica-se que nem as regras clássicas nem as de lógica livre para os quantificadores são aceitáveis. (O problema não pode ser resolvido enfraquecendo a regra de substituição pela identidade. ) Uma solução para este problema é empregar um tratamento mais geral dos quantificadores, onde o domínio de quantificação contém conceitos individuais em vez de objetos. Esta interpretação mais geral proporciona uma melhor combinação entre o tratamento de termos e o tratamento de quantificadores e resultados em sistemas adequados para regras lógicas clássicas ou livres (dependendo se os domínios fixos ou os domínios mundiais são escolhidos). Ele também fornece uma linguagem com potências expressivas fortes e muito necessárias (Bressan, 1973, Belnap e Müller, 2013a, 2013b), Esta interpretação mais geral proporciona uma melhor combinação entre o tratamento de termos e o tratamento de quantificadores e resultados em sistemas adequados para regras lógicas clássicas ou livres (dependendo se os domínios fixos ou os domínios mundiais são escolhidos). Ele também fornece uma linguagem com potências expressivas fortes e muito necessárias (Bressan, 1973, Belnap e Müller, 2013a, 2013b), Esta interpretação mais geral proporciona uma melhor combinação entre o tratamento de termos e o tratamento de quantificadores e resultados em sistemas adequados para regras lógicas clássicas ou livres (dependendo se os domínios fixos ou os domínios mundiais são escolhidos). Ele também fornece uma linguagem com potências expressivas fortes e muito necessárias (Bressan, 1973, Belnap e Müller, 2013a, 2013b),
Bibliografia
- Anderson, A. e N. Belnap, 1975, 1992, Entailment: The Logic of Pertinence and Necessity , vol. 1 (1975), vol. 2 (1992), Princeton: Princeton University Press.
- Barcan (Marcus), R., 1947, "Um cálculo funcional da primeira ordem com base na Implicação rigorosa", Journal of Symbolic Logic , 11: 1-16.
- ---, 1967, "Essentialism in Modal Logic" , Noûs , 1: 91-96.
- ---, 1990, "Um olhar para trás das animadversões de Quine sobre Modalidades", em R. Bartrett e R. Gibson (eds.), Perspectives on Quine , Cambridge: Blackwell.
- Belnap, N., M. Perloff e M. Xu, 2001, Enfrentando o Futuro , Nova York: Oxford University Press.
- Belnap, N. e T. Müller, 2013a, "CIFOL: Uma Lógica de Primeira Ordem Intensional de Caso (I): Rumo a uma Lógica de Títulos", Journal of Philosophical Logic , doi: 10.1007 / s10992-012-9267-x
- ---, 2013b, "BH-CIFOL: Uma Lógica de Primeira Ordem Intensional de Caso (II): Histórias de Ramificação," Journal of Philosophical Logic , doi: 10.1007 / s10992-013-9292-4
- Bencivenga, E., 1986, "Free Logics", em D. Gabbay e F. Guenthner (eds.), Handbook of Philosophical Logic , III.6, Dordrecht: D. Reidel, 373-426.
- Benthem, JF van, 1982, The Logic of Time , Dordrecht: D. Reidel.
- ---, 1983, Lógica Modal e Lógica Clássica , Nápoles: Bibliopolis.
- ---, 2010, Modal Logic for Open Minds , Stanford: CSLI Publications.
- Blackburn, P., com M. de Rijke e Y. Venema, 2001, Modal Logic , Cambridge: Cambridge University Press.
- Blackburn, P., com J. van Bentham e F. Wolter, 2007, Handbook of Modal Logic , Amsterdam: Elsevier.
- Bonevac, D., 1987, Dedução , Parte II, Palo Alto: Mayfield Publishing Company.
- Boolos, G., 1993, The Logic of Provability , Cambridge: Cambridge University Press.
- Bressan, A., 1973, A General Interpreted Modal Calculus , New Haven: Yale University Press.
- Bull, R. e K. Segerberg, 1984, "Basic Modal Logic", em D. Gabbay e F. Guenthner (eds.), Handbook of Philosophical Logic , II.1, Dordrecht: D. Reidel, 1-88.
- Carnap, R., 1947, Significado e Necessidade , Chicago: U. Chicago Press.
- Carnielli, W. e C. Pizzi, 2008, Modalidades e Multimodalidades , Heidelberg: Springer-Verlag.
- Chagrov, A. e M. Zakharyaschev, 1997, Modal Logic , Oxford: Oxford University Press.
- Chalmers, D., 1996, The Conscious Mind , Nova York: Oxford University Press.
- ---, 2002, "The Components of Content", em D. Chalmers (ed.), Philosophy of Mind: Leituras clássicas e contemporâneas , Oxford: Oxford University Press, 608-633.
- ---, 2006, "The Foundations of Two-Dimensional Semantics", em M. Garcia-Carpintero e J. Macia, Semântica bidimensional : Fundações e Aplicações , Oxford: Oxford University Press, 55-140.
- Chellas, B., 1980, Modal Logic: An Introduction , Cambridge: Cambridge University Press.
- Cresswell, MJ, 2001, "Modal Logic", em L. Goble (ed.), The Blackwell Guide to Philosophical Logic , Oxford: Blackwell, 136-158.
- ---, 1991, "Na Defesa da Fórmula Barcan", Logique et Analyse , 135-136: 271-282.
- ---, 1995, "Incompleteness and the Barcan formula", Journal of Philosophical Logic , 24: 379-403.
- Cocchiarella, N. e M. Freund, 2008, Lógica Modal Uma Introdução à sua Sintaxe e Semântica , Nova York: Oxford.
- Corsi, G., 2002, "Um teorema de integridade completo para lógicas modais quantificadas", Journal of Symbolic Logic , 67: 1483-1510.
- Crossley, J e L. Humberstone, 1977, "A Lógica da Actualidade", Relatórios sobre Lógica Matemática , 8: 11-29.
- Fitting, M. e R. Mendelsohn, 1998, First Order Modal Logic , Dordrecht: Kluwer.
- Gabbay, D., 1976, Investigações em Lógicas Modais e Tensas , Dordrecht: D. Reidel.
- ---, 1994, Lógica Temporal: Fundamentos Matemáticos e Aspectos Computacionais , Nova York: Oxford University Press.
- Garson, J., 2001, "Quantification in Modal Logic", em D. Gabbay e F. Guenthner (eds.) Handbook of Philosophical Logic , segunda edição, volume 3, Dordrecht: D. Reidel, 267-323.
- ---, 2005, "Unifying Quantified Modal Logic", Journal of Philosophical Logic , 34: 621-649.
- ---, 2013, Modal Logic for Philosophers, Segunda edição , Cambridge: Cambridge University Press.
- Goldblatt, R., 1993, Matemática da Modalidade , CSLI Lecture Notes # 43, Chicago: University of Chicago Press.
- ---, 2006, "Lógica Modal Matemática: uma Visão de sua Evolução", em D. Gabbay e J. Woods (eds.), Handbook of the History of Logic , vol. 6, Amsterdã: Elsevier.
- Harel, D., 1984, "Dynamic Logic", em D. Gabbay e F. Guenthner (eds.), Handbook of Philosophical Logic , II.10, Dordrecht: D. Reidel, 497-604.
- Hintikka, J., 1962, Knowledge and Belief: Uma introdução à lógica das duas noções , Ithaca, NY: Cornell University Press.
- Hilpinen, R., 1971, Deontic Logic: Leituras introdutórias e sistemáticas , Dordrecht: D. Reidel.
- Hughes, G. e M. Cresswell, 1968, Uma introdução à lógica modal , Londres: Methuen.
- ---, 1984, Um Companheiro para Modal Logic , Londres: Methuen.
- ---, 1996, Uma Nova Introdução à Lógica Modal , Londres: Routledge.
- Kaplan, D., 1989, "Demonstratives", em Temas de Kaplan , Oxford: Oxford University Press.
- Kripke, S., 1963, "Considerações semânticas sobre lógica modal", Acta Philosophica Fennica , 16: 83-94.
- ---, 1980, Naming and Necessity , Cambridge, MA: Harvard University Press.
- Konyndik, K., 1986, Lógica Modal Introdutória , Notre Dame: University of Notre Dame Press.
- Kvart, I., 1986, A Theory of Counterfactuals , Indianapolis: Hackett Publishing Company.
- Lemmon, E. e D. Scott, 1977, Uma introdução à lógica modal , Oxford: Blackwell.
- Lewis, CI e CH Langford, 1959 (1932), Symbolic Logic , New York: Dover Publications.
- Lewis, D., 1973, Counterfactuals , Cambridge, MA: Harvard University Press.
- Linsky, B. e E. Zalta, 1994, "Em defesa da lógica modal quantificada mais simples" , Perspectivas filosóficas , (Lógica e linguagem), 8: 431-458.
- Mares, E., 2004, lógica relevante: uma interpretação filosófica , Cambridge: Cambridge University Press.
- Mints, G. 1992, Uma breve introdução ao Modal Logic , Chicago: University of Chicago Press.
- Ponse, A., com M. de Rijke e Y. Venema, 1995, Lógica Modal e Álgebra de Processo, Uma Perspectiva de Bisimulação , Stanford: CSLI Publications.
- Popkorn, S., 1995, Primeiros Passos na Lógica Modal , Cambridge: Cambridge University Press.
- Prior, AN, 1957, Time and Modality , Oxford: Clarendon Press.
- ---, 1967, passado, presente e futuro , Oxford: Clarendon Press.
- Quine, WVO, 1953, "Referência e Modalidade", em From a Logical Point of View , Cambridge, MA: Harvard University Press. 139-159.
- Rescher, N, e A. Urquhart, 1971, Temporal Logic , Nova York: Springer Verlag.
- Sahlqvist, H., 1975, "Completude e Correspondência na Semântica da Primeira e Segunda Ordem para a Lógica Modal", em S. Kanger (ed.), Procedimentos do Terceiro Simpósio da Lógica Escandinava , Amsterdã: Holanda do Norte. 110-143.
- Thomason, R., 1984, "Combinações de Tens e Modalidade", em D. Gabbay e F. Guenthner (eds.), Handbook of Philosophical Logic , II.3, Dordrecht: D. Reidel, 135-165.
- Zeman, J., 1973, Modal Logic, The Lewis-Modal Systems , Oxford: Oxford University Press.
- Anderson, A. e N. Belnap, 1975, 1992, Entailment: The Logic of Pertinence and Necessity , vol. 1 (1975), vol. 2 (1992), Princeton: Princeton University Press.
- Barcan (Marcus), R., 1947, "Um cálculo funcional da primeira ordem com base na Implicação rigorosa", Journal of Symbolic Logic , 11: 1-16.
- ---, 1967, "Essentialism in Modal Logic" , Noûs , 1: 91-96.
- ---, 1990, "Um olhar para trás das animadversões de Quine sobre Modalidades", em R. Bartrett e R. Gibson (eds.), Perspectives on Quine , Cambridge: Blackwell.
- Belnap, N., M. Perloff e M. Xu, 2001, Enfrentando o Futuro , Nova York: Oxford University Press.
- Belnap, N. e T. Müller, 2013a, "CIFOL: Uma Lógica de Primeira Ordem Intensional de Caso (I): Rumo a uma Lógica de Títulos", Journal of Philosophical Logic , doi: 10.1007 / s10992-012-9267-x
- ---, 2013b, "BH-CIFOL: Uma Lógica de Primeira Ordem Intensional de Caso (II): Histórias de Ramificação," Journal of Philosophical Logic , doi: 10.1007 / s10992-013-9292-4
- Bencivenga, E., 1986, "Free Logics", em D. Gabbay e F. Guenthner (eds.), Handbook of Philosophical Logic , III.6, Dordrecht: D. Reidel, 373-426.
- Benthem, JF van, 1982, The Logic of Time , Dordrecht: D. Reidel.
- ---, 1983, Lógica Modal e Lógica Clássica , Nápoles: Bibliopolis.
- ---, 2010, Modal Logic for Open Minds , Stanford: CSLI Publications.
- Blackburn, P., com M. de Rijke e Y. Venema, 2001, Modal Logic , Cambridge: Cambridge University Press.
- Blackburn, P., com J. van Bentham e F. Wolter, 2007, Handbook of Modal Logic , Amsterdam: Elsevier.
- Bonevac, D., 1987, Dedução , Parte II, Palo Alto: Mayfield Publishing Company.
- Boolos, G., 1993, The Logic of Provability , Cambridge: Cambridge University Press.
- Bressan, A., 1973, A General Interpreted Modal Calculus , New Haven: Yale University Press.
- Bull, R. e K. Segerberg, 1984, "Basic Modal Logic", em D. Gabbay e F. Guenthner (eds.), Handbook of Philosophical Logic , II.1, Dordrecht: D. Reidel, 1-88.
- Carnap, R., 1947, Significado e Necessidade , Chicago: U. Chicago Press.
- Carnielli, W. e C. Pizzi, 2008, Modalidades e Multimodalidades , Heidelberg: Springer-Verlag.
- Chagrov, A. e M. Zakharyaschev, 1997, Modal Logic , Oxford: Oxford University Press.
- Chalmers, D., 1996, The Conscious Mind , Nova York: Oxford University Press.
- ---, 2002, "The Components of Content", em D. Chalmers (ed.), Philosophy of Mind: Leituras clássicas e contemporâneas , Oxford: Oxford University Press, 608-633.
- ---, 2006, "The Foundations of Two-Dimensional Semantics", em M. Garcia-Carpintero e J. Macia, Semântica bidimensional : Fundações e Aplicações , Oxford: Oxford University Press, 55-140.
- Chellas, B., 1980, Modal Logic: An Introduction , Cambridge: Cambridge University Press.
- Cresswell, MJ, 2001, "Modal Logic", em L. Goble (ed.), The Blackwell Guide to Philosophical Logic , Oxford: Blackwell, 136-158.
- ---, 1991, "Na Defesa da Fórmula Barcan", Logique et Analyse , 135-136: 271-282.
- ---, 1995, "Incompleteness and the Barcan formula", Journal of Philosophical Logic , 24: 379-403.
- Cocchiarella, N. e M. Freund, 2008, Lógica Modal Uma Introdução à sua Sintaxe e Semântica , Nova York: Oxford.
- Corsi, G., 2002, "Um teorema de integridade completo para lógicas modais quantificadas", Journal of Symbolic Logic , 67: 1483-1510.
- Crossley, J e L. Humberstone, 1977, "A Lógica da Actualidade", Relatórios sobre Lógica Matemática , 8: 11-29.
- Fitting, M. e R. Mendelsohn, 1998, First Order Modal Logic , Dordrecht: Kluwer.
- Gabbay, D., 1976, Investigações em Lógicas Modais e Tensas , Dordrecht: D. Reidel.
- ---, 1994, Lógica Temporal: Fundamentos Matemáticos e Aspectos Computacionais , Nova York: Oxford University Press.
- Garson, J., 2001, "Quantification in Modal Logic", em D. Gabbay e F. Guenthner (eds.) Handbook of Philosophical Logic , segunda edição, volume 3, Dordrecht: D. Reidel, 267-323.
- ---, 2005, "Unifying Quantified Modal Logic", Journal of Philosophical Logic , 34: 621-649.
- ---, 2013, Modal Logic for Philosophers, Segunda edição , Cambridge: Cambridge University Press.
- Goldblatt, R., 1993, Matemática da Modalidade , CSLI Lecture Notes # 43, Chicago: University of Chicago Press.
- ---, 2006, "Lógica Modal Matemática: uma Visão de sua Evolução", em D. Gabbay e J. Woods (eds.), Handbook of the History of Logic , vol. 6, Amsterdã: Elsevier.
- Harel, D., 1984, "Dynamic Logic", em D. Gabbay e F. Guenthner (eds.), Handbook of Philosophical Logic , II.10, Dordrecht: D. Reidel, 497-604.
- Hintikka, J., 1962, Knowledge and Belief: Uma introdução à lógica das duas noções , Ithaca, NY: Cornell University Press.
- Hilpinen, R., 1971, Deontic Logic: Leituras introdutórias e sistemáticas , Dordrecht: D. Reidel.
- Hughes, G. e M. Cresswell, 1968, Uma introdução à lógica modal , Londres: Methuen.
- ---, 1984, Um Companheiro para Modal Logic , Londres: Methuen.
- ---, 1996, Uma Nova Introdução à Lógica Modal , Londres: Routledge.
- Kaplan, D., 1989, "Demonstratives", em Temas de Kaplan , Oxford: Oxford University Press.
- Kripke, S., 1963, "Considerações semânticas sobre lógica modal", Acta Philosophica Fennica , 16: 83-94.
- ---, 1980, Naming and Necessity , Cambridge, MA: Harvard University Press.
- Konyndik, K., 1986, Lógica Modal Introdutória , Notre Dame: University of Notre Dame Press.
- Kvart, I., 1986, A Theory of Counterfactuals , Indianapolis: Hackett Publishing Company.
- Lemmon, E. e D. Scott, 1977, Uma introdução à lógica modal , Oxford: Blackwell.
- Lewis, CI e CH Langford, 1959 (1932), Symbolic Logic , New York: Dover Publications.
- Lewis, D., 1973, Counterfactuals , Cambridge, MA: Harvard University Press.
- Linsky, B. e E. Zalta, 1994, "Em defesa da lógica modal quantificada mais simples" , Perspectivas filosóficas , (Lógica e linguagem), 8: 431-458.
- Mares, E., 2004, lógica relevante: uma interpretação filosófica , Cambridge: Cambridge University Press.
- Mints, G. 1992, Uma breve introdução ao Modal Logic , Chicago: University of Chicago Press.
- Ponse, A., com M. de Rijke e Y. Venema, 1995, Lógica Modal e Álgebra de Processo, Uma Perspectiva de Bisimulação , Stanford: CSLI Publications.
- Popkorn, S., 1995, Primeiros Passos na Lógica Modal , Cambridge: Cambridge University Press.
- Prior, AN, 1957, Time and Modality , Oxford: Clarendon Press.
- ---, 1967, passado, presente e futuro , Oxford: Clarendon Press.
- Quine, WVO, 1953, "Referência e Modalidade", em From a Logical Point of View , Cambridge, MA: Harvard University Press. 139-159.
- Rescher, N, e A. Urquhart, 1971, Temporal Logic , Nova York: Springer Verlag.
- Sahlqvist, H., 1975, "Completude e Correspondência na Semântica da Primeira e Segunda Ordem para a Lógica Modal", em S. Kanger (ed.), Procedimentos do Terceiro Simpósio da Lógica Escandinava , Amsterdã: Holanda do Norte. 110-143.
- Thomason, R., 1984, "Combinações de Tens e Modalidade", em D. Gabbay e F. Guenthner (eds.), Handbook of Philosophical Logic , II.3, Dordrecht: D. Reidel, 135-165.
- Zeman, J., 1973, Modal Logic, The Lewis-Modal Systems , Oxford: Oxford University Press.
Comentários
Postar um comentário