LÓGICA EPISTÊMICA: UMA INTRODUÇÃO

LÓGICA EPISTEMOLOGICA
(EPISTÊMICA)

UMA INTRODUÇÃO PELO MÉTODO DINÂMICO

VINICIUS DIAS DE SOUZA

Lógica epistemológica dinâmica

Este artigo conta a história do surgimento da lógica epistêmica dinâmica. O surgimento começou na década de 1960 com a criação e o desenvolvimento da lógica epistêmica, a lógica do conhecimento. Então, no final dos anos 80, surgiu a lógica epistêmica dinâmica, a lógica da mudança de conhecimento. Grande parte disso foi motivada por enigmas e paradoxos.

O número de pesquisadores ativos nessas lógicas cresce significativamente todos os anos porque há tantas relações e aplicações para ciência da computação, sistemas multi-agentes, filosofia e ciência cognitiva.

Os operadores de conhecimento modal na lógica epistêmica são formalmente interpretados empregando relações de acessibilidade binária em modelos Kripke multi-agentes (estruturas relacionais), onde essas relações devem ser relações de equivalência para respeitar as propriedades do conhecimento. Os operadores de mudança de conhecimento correspondem a outro tipo de modalidade, mais semelhante a uma modalidade dinâmica. Uma peculiaridade desta modalidade dinâmica é que ela é interpretada transformando as estruturas de Kripke usadas para interpretar o conhecimento e não, pelo menos não à primeira vista, por uma relação de acessibilidade dada com um modelo Kripke. Embora chamado de "lógica epistêmica dinâmica", essa lógica modal de dois ordenamentos se aplica a configurações mais gerais do que a lógica do conhecimento meramente S5.

O presente artigo discute em profundidade a história inicial da lógica epistêmica dinâmica. Em seguida, menciona brevemente uma série de desenvolvimentos mais recentes envolvendo mudanças factuais, uma (de várias) traduções padrão para a lógica epistêmica temporal e uma relação com o cálculo da situação (um quadro bem conhecido na inteligência artificial para representar a mudança). É dada especial atenção à relevância da lógica epistêmica dinâmica para a revisão da crença, para a teoria da fala e para a lógica filosófica. A parte na lógica filosófica presta atenção às frases de Moore, ao paradoxo de Fitch e ao exame de surpresa.

I. Introdução

Nesta visão, contamos a história do surgimento da lógica epistêmica dinâmica. É um pouco presuncioso chamá-lo de um aumento, mas só podemos observar esse fenômeno bastante peculiar. O número de pesquisadores ativos nessas lógicas cresce todos os anos porque existem tantas relações com ciência da computação, sistemas multi-agentes, filosofia e ciência cognitiva. Tudo começou com a lógica do conhecimento na década de 1960, e grande parte disso foi motivada por quebra-cabeças e paradoxos.

A lógica dinâmica é a lógica da mudança de conhecimento. O ponto de partida da lógica epistêmica dinâmica (DEL) é, portanto, a lógica do conhecimento. Uma publicação fundadora é [42]. Nós nos referimos a [41] para uma visão geral da lógica e das referências epistêmicas. Uma característica chave da lógica epistêmica é que o estado da informação de vários agentes pode ser representado por um modelo Kripke. Dado um conjunto de agentes e um conjunto de variáveis ​​proposicionais, um modelo de Kripke consiste em um conjunto de estados, um conjunto de relações de acessibilidade (cada uma uma relação binária no domínio), ou seja, um para cada agente e uma avaliação (que conta quais variáveis ​​proposicionais são verdadeiras em que estados). Na lógica epistêmica, o conjunto de estados de um modelo de Kripke é interpretado como um conjunto de alternativas epistêmicas.R α . Um agente α sabe  que uma proposição φ é verdadeira no estado a de um modelo Kripke M ( M; a ⊨ K α φ ), se e somente se essa proposição φ for verdadeira em todos os estados que o agente α considere possíveis nesse estado (isto é, que são R α -acessíveis de a ). Uma proposição conhecida pelo agente α pode pertencer ao conhecimento de algum agente (por exemplo, se considerar a fórmula K α K βψ). Desta forma, um modelo Kripke com relações de acessibilidade para todos os agentes representa a informação (de ordem superior) de todos os agentes relevantes simultaneamente.

Em DEL, a mudança de informação é modelada pela transformação de modelos Kripke. Como a DEL é principalmente sobre mudanças de informação devido à comunicação, as transformações do modelo normalmente não envolvem mudanças factuais. Os fatos físicos nus do mundo permanecem inalterados, mas a informação dos agentes sobre o mundo muda. Em termos de modelos Kripke, isso significa que as relações de acessibilidade dos agentes precisam mudar (e conseqüentemente o conjunto de estados do modelo também pode mudar). Os operadores modais em línguas epistêmicas dinâmicas denotam essas transformações do modelo. A relação de acessibilidade associada a esses operadores não é uma dentro do modelo Kripke, mas pertence à relação de transformação entre os modelos Kripke, conforme o exemplo da próxima seção será mostrado.

Na Seção 2 é apresentado um cenário de exemplo que pode ser capturado pelo DEL. Na Seção 3, é apresentada uma visão geral histórica das principais abordagens em DEL, com detalhes sobre suas técnicas de modelagem. A Seção 4 discute como modelar revisão de crenças em DEL. A seção 5 conecta idéias entre a teoria do ato de fala e DEL. Finalmente, a Seção 6 é sobre a relação entre DEL e filosofia: trata das orações de Moore, do paradoxo de Fitch e do Exame de Surpresa.

II. Um cenário de exemplo

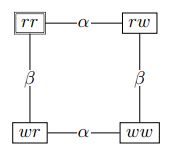
Figura 1: Um modelo Kripke para a situação em que dois agentes recebem um cartão vermelho ou branco.

Considere o seguinte cenário: Ann e Bob recebem um cartão vermelho ou branco de um lado (o lado da face) e indescritível do outro lado (lado traseiro). Eles só vêem seu próprio cartão e, portanto, eles ignoram o cartão do outro agente. Existem quatro possibilidades: ambos possuem cartões brancos, ambos têm cartões vermelhos, Ann tem um cartão branco e Bob tem um cartão vermelho ou vice-versa. Estes são os estados do modelo e são representados por nomes informativos como rw , significando que Ann recebeu um cartão vermelho ( r ) e Bob recebeu um cartão branco ( w ). Deixe-nos assumir que ambos têm cartões vermelhos, isto é, deixe o estado atual ser rr . Isso é indicado pelas duplas linhas em torno do estado rrna Figura 1. Os estados do modelo Kripke são conectados por linhas, que são rotuladas (α ou β, denotando Ann ou Bob, respectivamente) para indicar que os agentes não podem distinguir os estados assim conectados. (Para ser completo, também deve ser indicado que nenhum estado pode ser distinguido de si. Para legibilidade, essas "linhas reflexivas" não são desenhadas, mas, de fato, as relações de acessibilidade R α  e R β são relações de equivalência, uma vez que a indistinguibilidade epistêmica é reflexiva, simétrica e transitiva.) No modelo da Figura 1, não existem linhas α entre os estados em que Ann possui cartas diferentes, ou seja, ela pode distinguir os estados no topo, onde ela tem um cartão vermelho, daqueles que estão no fundo, onde ela tem um branco. Da mesma forma, Bob é capaz de distinguir a metade esquerda da metade direita do modelo. Isso representa a circunstância de que Ann e Bob conhecem a cor de seu próprio cartão, mas não a cor do outro cartão. No modelo Kripke da Figura 1, também vemos que a informação de ordem superior está representada corretamente. Ambos os agentes sabem que o outro agente conhece a cor do seu cartão, e eles sabem que eles sabem disso, e assim por diante.

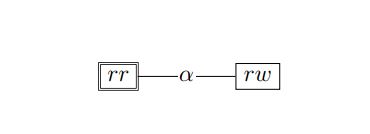
Figura 2: Um modelo de Kripke para a situação depois que Ann lhe diz que ela tem um cartão vermelho.

                                    

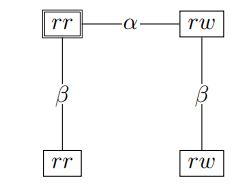
Figura 3: Um modelo Kripke para a situação depois que Ann poderia ter olhado o cartão de Bob.

Suponha que depois de pegar suas cartas, Ann diz com sinceridade a Bob "Eu tenho um cartão vermelho". O modelo Kripke que representa a situação resultante é exibido na Figura 2. Agora, ambos os agentes sabem que Ann tem um cartão vermelho, e eles sabem que eles sabem que ela tem um cartão vermelho, e assim por diante: é um conhecimento comum entre eles. (Uma fórmula φ é conhecimento comum entre um grupo de agentes se todos no grupo sabem que φ, todos sabem que todos sabem que φ, e assim por diante.) Portanto, não há mais necessidade de estados em que Ann tenha um cartão branco, então aqueles não aparecem no modelo Kripke. Note-se que, no novo modelo Kripke, não há mais nenhuma linha rotulada como β. Não importa como as cartas foram distribuídas, Bob só considera um estado possível: o atual. Na verdade, Bob está agora totalmente informado.

Agora que Bob conhece a cor do cartão de Ann, Bob coloca o cartão com a mão embaixo na mesa e sai da sala por um momento. Quando ele retorna, ele considera possível que Ann olhasse seu cartão, mas também que não o fez. Supondo que ela não olhou, o modelo de Kripke que representa a situação resultante é o mostrado na Figura 3. Em contraste com o modelo anterior, existem neste modelo linhas para Bob novamente. Isso porque ele não está mais completamente informado sobre a situação. Ele não sabe se Ann conhece a cor do seu cartão, mas ele ainda sabe que tanto Ann quanto ele tem um cartão vermelho. Somente suas informações de ordem superior mudaram. Ann, por outro lado, sabe se ela olhou para o cartão de Bob e também sabe se ela conhece a cor do cartão de Bob. Ela também sabe que Bob considera possível que conheça a cor do seu cartão. No modelo da Figura 3, vemos que dois estados que representam a mesma informação factual podem diferir em virtude das linhas que os conectam a outros estados: o estadorr na parte superior e rr na parte inferior apenas diferem em informações de ordem superior.

Nesta seção, vimos duas maneiras pelas quais a mudança de informação pode ocorrer. Passando do primeiro modelo para o segundo, a mudança de informação foi pública, no sentido de que todos os agentes receberam a mesma informação. Passar do segundo para o terceiro modelo envolveu a mudança de informação onde nem todos os agentes tinham a mesma informação, porque Bob não sabia se Ann olhava seu cartão enquanto ele estava ausente. A tarefa de DEL é fornecer uma lógica com a qual descrever esses tipos de mudança de informação.

III. Uma história de DEL

DEL não surgiu em um vácuo científico. O "turno dinâmico" em lógica e semântica ([72], [34] e [60]) DEL muito inspirado, e o próprio DEL também pode ser visto como uma parte da curva dinâmica. O aparelho formal de DEL é muito parecido com lógica dinâmica proposicional (PDL) [40] e lógica dinâmica quantificada (QDL) [39]. Há também uma relação com a atualização de semântica (US) [36, 93] - nem todas as fórmulas são interpretadas dinamicamente, como lá, mas as fórmulas e atualizações são claramente distinguidas.

O estudo da lógica epistêmica na ciência da computação e AI levou ao desenvolvimento da lógica temporal epistemológica (ETL) para modelar a mudança de informação em sistemas multi-agente (ver [25] e [55]). Ao invés de modificação do modelo por operadores modais que transformam o modelo, a mudança é modelada pela progressão do tempo nessas abordagens. No entanto, os tipos de fenômenos estudados por ETL e DEL se sobrepõem em grande parte.

Após este breve esboço do contexto em que o DEL foi desenvolvido, o restante da seção se concentra no desenvolvimento de suas duas abordagens principais. A primeira é a lógica do anúncio público, que é apresentada na Seção 3.1. O segundo, apresentado na Seção 3.2, é a abordagem dominante em DEL (às vezes identificado com DEL).

uma. Anúncios

A publicação original: Plaza A primeira lógica epistêmica dinâmica, chamada lógica de anúncio público (PAL), foi desenvolvida pela Plaza em [61]. Isto foi publicado em 1989. O exemplo em que Ann diz a Bob que ela possui um cartão vermelho é um exemplo de anúncio público. Um anúncio público é um evento comunicativo em que todos os agentes recebem a mesma informação e é de conhecimento comum que é assim. O idioma de PAL é dado pelo seguinte formulário Backus-Naur:

Além da linguagem proposicional usual, K α φ é lido como o agente α sabe que φ, e [φ] ψ é lido como depois de φ ser anunciado ψ é o caso. No exemplo acima, poderíamos, por exemplo, traduzir "Depois de anunciar que Ann tem um cartão vermelho, Bob sabe que Ann tem um cartão vermelho" como [r α ] K β r α .

Um anúncio é modelado pela remoção dos estados onde o anúncio é falso, ou seja, indo para um submodelo. Esta transformação do modelo é a característica principal da semântica do PAL.

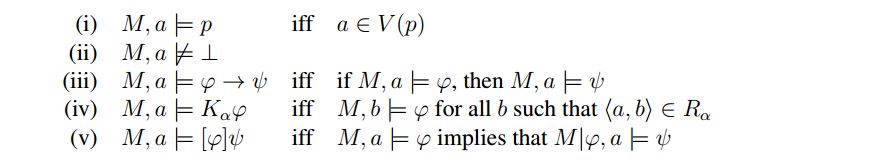
Na cláusula (v), a condição de que a fórmula anunciada seja verdadeira no estado atual implica que apenas anúncios verdadeiros podem ocorrer. O modelo MΙφ é o modelo obtido de M removendo todos os estados não-φ. O novo conjunto de estados consiste nos & Phi-membros da M . Conseqüentemente, as relações de acessibilidade, bem como a avaliação, são restritas a esses estados. As letras proposicionais verdadeiras em um estado permanecem verdadeiras após um anúncio. Isso reflete a idéia de que a comunicação só pode gerar mudanças de informação, e não mudanças factuais.

A abordagem de Gerbrandy e Groeneveld Uma lógica semelhante à PAL foi desenvolvida de forma independente por Gerbrandy e Groeneveld em [32], que é mais extensivamente tratada na tese de doutorado de Gerbrandy [30]. Existem três diferenças principais entre essa abordagem e a abordagem da Plaza. Em primeiro lugar, Gerbrandy e Groeneveld não usam modelos Kripke na semântica de sua língua. Em vez disso, eles usam estruturas chamadas de possibilidadesque são definidos por meio de uma teoria de conjuntos não bem-fundada [1], um ramo da teoria dos conjuntos onde o axioma da fundação é substituído por outro axioma. As possibilidades e os modelos Kripke estão intimamente ligados: as possibilidades correspondem às classes de bisimulação de modelos Kripke [18]. Mais tarde, Gerbrandy forneceu semântica sem usar uma teoria de conjuntos não bem-fundada para uma versão simplificada de sua lógica de anúncio público [31].

A segunda diferença é que Gerbrandy e Groeneveld também consideram anúncios que não são verdadeiros. Na sua opinião, uma lógica para anúncios deve modelar o que acontece quando as informações novas são consideradasverdadeiras pelos agentes. Portanto, de acordo com eles, o que acontece de ser verdade não merece nenhum status especial. Isso é mais parecido com a noção de atualização nos EUA. Em termos de modelos Kripke, isso significa que, atualizando, os agentes podem não considerar mais o estado atual, ou seja,  R α pode não ser mais reflexivo. Em certo sentido, seria mais preciso chamar essa lógica de um doxástico dinâmico lógica (uma lógica dinâmica de crença) ao invés de uma lógica epistêmica dinâmica, pois, de acordo com a maioria das teorias, o conhecimento implica a verdade, enquanto que as crenças não precisam ser verdadeiras.

Em terceiro lugar, sua lógica é mais geral no sentido de que os anúncios de subgrupos são tratados (onde apenas um subgrupo do grupo de todos os agentes adquire novas informações); e especialmente anúncios privados são considerados, onde apenas um agente obtém informações. Esses anúncios são modelados de tal forma que os agentes que não recebem informações nem sequer consideram possível que alguém tenha aprendido alguma coisa. Em termos de modelos Kripke, esta é outra maneira pela qual R α pode perder reflexividade.

Adicionando conhecimento comumSemântica para anúncios públicos, grupais e privados usando modelos Kripke foi proposta por Baltag, Moss e Solecki em [14]. Esta semântica é equivalente à semântica de Gerbrandy (como foi mostrado em [58]). O principal contributo em [14] para PAL foi que sua abordagem também abrangeu conhecimento comum, que é um conceito importante quando alguém está interessado em informações de ordem superior e desempenha um papel importante na interação social (ver [92]). A inclusão do conhecimento comum coloca uma série de problemas técnicos.

b. Outros Eventos Informativos

Abordagem de Groeneveld e Gerbrandy Além de uma lógica para anúncios Gerbrandy também desenvolveu um sistema para mudanças de informação mais gerais envolvendo muitos agentes, cada um dos quais pode ter uma perspectiva diferente. Este é, por exemplo, o caso em que Ann pode olhar para o cartão de Bob.

Para modelar essa mudança de informação, é importante perceber que diferentes níveis de informação não são claramente representados em um modelo Kripke. Por exemplo, o que Ann realmente sabe sobre os cartões depende de R α , mas o que Bob sabe sobre o que Ann sabe sobre os cartões depende de R α também. Portanto, mudar algo no modelo Kripke, como cortar uma linha, muda a informação em muitos níveis. Para enfrentar esta questão, realmente vale a pena usar semânticas não bem-fundadas. Uma das maneiras de pensar sobre as possibilidades definidas por Gerbrandy e Groeneveld é como árvores infinitas. Em tal árvore, diferentes níveis de informação são representados por certos caminhos na árvore. Ao manipular a parte apropriada da árvore, pode-se alterar a informação dos agentes no nível apropriado. Essa percepção vem de Groeneveld [37] e também foi usada por Renardel de Lavalette em [62], que apresenta estruturas modais magra detreel usando a teoria de conjuntos comuns na semântica de uma lógica epistêmica dinâmica.

Abordagem de Van Ditmarsch Inspirada pelo trabalho de Gerbrandy e Groeneveld, Van Ditmarsch desenvolveu uma lógica epistêmica dinâmica para modelar mudanças de informação em jogos de conhecimento, onde o objetivo dos jogadores é obter conhecimento de algum aspecto do jogo. Clue e Battleships são exemplos típicos de jogos de conhecimento. Os jogadores nunca são enganados em tais jogos e, portanto, a lógica epistêmica dinâmica de Gerbrandy e Groeneveld em que a reflexividade pode ser perdida parece inadequada. No Ph.D. de Van Ditmarsch. tese [86], uma lógica é apresentada onde todas as transformações do modelo são de modelos Kripke com relações de equivalência para modelos de Kripke com relações de equivalência, o que é, portanto, adaptado à mudança de informação envolvendo conhecimento. Esta abordagem foi ainda simplificada por Van Ditmarsch em [87] e posteriormente estendida para incluir ações simultâneas (quando dois ou mais eventos ocorrem ao mesmo tempo) em [90]. Um dos problemas abertos dessas lógicas é que não foi obtida uma prova de integridade para os sistemas axiom.

A abordagem dominante: Baltag, Moss e SoleckiOutra maneira de modelar eventos informativos complexos foi desenvolvida por [14], que se tornou a abordagem dominante em DEL. Sua abordagem é altamente intuitiva e está deitada na base de muitos trabalhos no campo: de fato, muitos se referem a essa abordagem simplesmente como DEL. Sua visão chave era que os eventos de mudança de informações podem ser modelados da mesma forma que situações envolvendo informações. Dada uma situação, como quando Ann e Bob cada um têm um cartão, pode-se facilmente fornecer um modelo Kripke para tal situação. Simplesmente considera quais estados podem ocorrer e quais desses estados os agentes não podem distinguir. Pode-se fazer o mesmo com eventos envolvendo informações. Dado um cenário, como Ann, possivelmente, olhando para o cartão de Bob, pode-se determinar quais eventos podem ocorrer: ou ela parece e vê que é vermelha (ela aprende que rβ) ou ela vê que é branca (ela aprende que wβ ), ou ela não olha o cartão (ela não aprende nada novo, indicado pela tautologia Τ). É claro que Ann pode distinguir esses eventos particulares, mas Bob não pode. Tais modelos são chamados de modelos de ação ou de eventos.

Um evento m odel A é um triplo 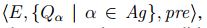 consistindo de um conjunto de eventos E , uma relação binária  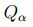sobre E para cada agente e uma função de pré-condição  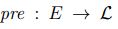que atribui uma fórmula a cada evento. Esta pré-condição determina em que circunstâncias o evento pode realmente ocorrer. Ann só pode dizer com sinceridade que ela tem um cartão vermelho, se na verdade ela tiver um cartão vermelho. O modelo de evento para o evento onde Ann poderia ter olhado no cartão de Bob é

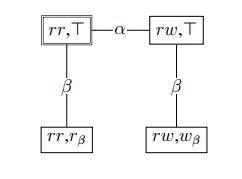
Figura 4: Um modelo de evento para quando Ann pode olhar para o cartão de Bob.

Figura 5: A atualização do produto para os modelos da Figura 3 e da Figura 4.

dado na Figura 4, onde cada evento é representado por sua pré-condição.

O modelo Kripke da situação após o evento é construído com um procedimento chamado atualização de produto . Para cada estado no modelo Kripke original, determina quais eventos podem ocorrer nesse estado (ou seja, determina se a condição prévia do evento é verdadeira nesse estado). O conjunto de estados do novo modelo consiste nos pares de estados e eventos ( a, e ), que representam o resultado do evento e queocorre no estado a. A nova relação de acessibilidade agora é fácil de determinar. Se dois estados fossem indistinguíveis para um agente e dois eventos também fossem indistinguíveis para esse agente, então o resultado desses eventos ocorrendo nesses estados também deveria ser indistinguível. Esta implicação também tem o contrário: se o resultado de dois eventos que acontecem em dois estados são indistinguíveis, então os estados e eventos originais também devem ser indistinguíveis. (Van Benthem [73] caracteriza atualização do produto como tendo memória perfeita , sem milagres , e uniformidade .) Os fatos básicos sobre o mundo não mudar devido a uma

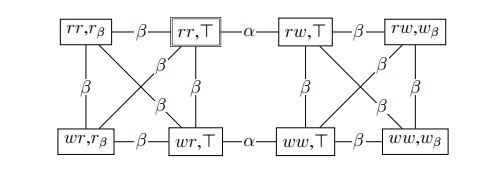
Figura 6: A atualização do produto para os modelos da Figura 1 e da Figura 4.

meramente evento comunicativo. E assim, a avaliação em < a, e > simplesmente segue a avaliação antiga em um .

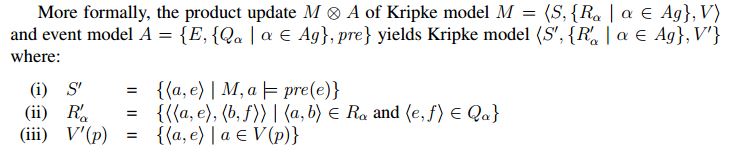
O modelo da Figura 5 é o resultado de uma atualização do modelo do modelo na Figura 2 e do modelo de eventos da Figura 4. Pode-se ver que isso é o mesmo que o modelo na Figura 3 (exceto os nomes dos estados) o que indica que a atualização do produto produz o resultado intuitivamente correto.

Pode-se perguntar se o modelo da Figura 4 representa o evento com precisão. De acordo com o modelo do evento, Bob considera possível que Ann olhe para o cartão e veja que é branco. Bob, no entanto, já sabe que o cartão é vermelho e, portanto, não deve considerar este evento possível. Esta crítica é justificada e pode-se construir um modelo de eventos que leve isso em conta, mas a beleza do modelo de evento é precisamente que é separada da informação dos agentes sobre o mundo, de tal forma que fornece um modelo preciso de apenas A informação que os agentes têm sobre o evento. Isso significa que a atualização do produto produz o resultado certo, independentemente do modelo Kripke da situação em que o evento ocorreu. Por exemplo, levando a atualização do produto com o modelo da Figura 1, produz o modelo de Kripke representado na Figura 6, o que representa a situação em que Ann poderia olhar para o cartão de Bob imediatamente após a entrega dos cartões. O modelo resultante também representa essa situação corretamente. Isso indica que em informações estáticas DEL e as informações dinâmicas podem ser separadas.

No idioma lógico do DEL, esses modelos de eventos aparecem como modalidades [ A, e ], onde e é considerado o evento que realmente ocorre. O idioma é dado pelo seguinte formulário Backus-Naur

As cláusulas (i) - (iv) são as mesmas que para PAL. Na cláusula (v) 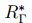 é o fechamento transitivo reflexivo da união das relações de acessibilidade de membros de Γ. A cláusula (vi) é uma cláusula padrão para modalidades dinâmicas, exceto que a relação de acessibilidade para modalidades dinâmicas é uma relação na classe de todos os modelos Kripke. Na cláusula (vii) é necessário que a pré-condição do modelo de evento seja verdadeira no estado atual, garantindo assim que < a, e>, o novo estado atual, exista na atualização do produto. As cláusulas (viii) e (ix) são a semântica usual para escolha não determinística e composição seqüencial.

Para acessar a parte seguinte, clique:

 [PARTE 2]