LÓGICA: SÍMBOLOS

Símbolos de lógica

Símbolo	Significado	Notas
Operadores (Conectivos)
¬	Negação (NÃO)	O tilde ( ~ ) também é freqüentemente usado.
∧	conjunção (AND)	O e comercial ( & ) ou o ponto ( · ) também são freqüentemente usados.
∨	disjunção (OR)	Esta é a disjunção inclusiva, equivalente e / ou em inglês.
⊕	Disjunção exclusiva (XOR)	⊕ significa que apenas uma das proposições conectadas é verdadeira, equivalente a ... ou.Às vezes ⊻ é usado.
\|	negação alternativa (NAND)	Significa "não ambos". Às vezes escrito como ↑
↓	negação conjunta (NOR)	Significa "nem / nem".
→	condicional (se / então)	Muitos especialistas utilizam o símbolo ⊃ em vez disso. Isso também é conhecido como implicação material.
↔	biconditional (iff)	Significa "se e somente se" ≡ às vezes é usado, mas este site reserva esse símbolo de equivalência.
Quantificadores
∀	quantificador universal	Significa "para todos", então ∀ xPxsignifica que Px é verdadeiro para cadax .
∃	quantificador existencial	Significa "existe", então ∃ xPx significa que Px é verdadeiro para pelo menos um x.
Relações
⊨	implicação	α ⊨ β significa que βsegue de α
≡	equivalência	Também ⇔. A equivalência é uma implicação bidirecional, portanto α ≡ βsignifica α β e β α .
⊢	provabilidade	Mostra inferência provável. α βsignifica que a partir de α podemos provar que β .
∴	assim sendo	Usou-se para significar a conclusão de um argumento.Normalmente, leva a significar implicação, mas geralmente é usada para apresentar argumentos em que as premissas não implicam dedutivamente a conclusão.
⊩	forças	Um relacionamento entre possíveis mundos e frases na lógica modal.
Verdade-Valores
⊤	tautologia	Pode ser usado para substituir qualquer fórmula tautologous (sempre verdadeira).
⊥	contradição	Pode ser usado para substituir qualquer fórmula contraditória (sempre falsa). Às vezes, "F" é usado.
Parênteses
()	parênteses	Usado para agrupar expressões para mostrar precedência de operações. Os suportes quadrados [] são usados às vezes para esclarecer agrupamentos.
Teoria de conjuntos
∈	associação	Indica adesão a um conjunto. Se a ∈ Γ, então a é um membro (ou um elemento) do conjunto Γ.
∪	União	Usado para juntar conjuntos. Se S e T são conjuntos de fórmulas, S ∪ T é um conjunto contendo todos os membros de ambos.
∩	interseção	A sobreposição entre conjuntos. Se S e T são conjuntos de fórmulas, S ∩ T é um conjunto que contém esses elementos que são membros de ambos.
⊆	subconjunto	Um subconjunto é um conjunto que contém alguns ou todos os elementos de outro conjunto.
⊂	subconjunto próprio	Um subconjunto apropriado contém alguns, mas não todos, elementos de outro conjunto.
=	estabelecer igualdade	Dois conjuntos são iguais se contiverem exatamente os mesmos elementos.
∁	complemento absoluto	∁ (S) é o conjunto de todas as coisas que não estão no conjunto de S. Por vezes escrito como C (S), S ou S ^C .
-	complemento relativo	T - S é o conjunto de todos os elementos em T que não estão também em S. Às vezes escrito comoT \ S .
∅	conjunto vazio	O conjunto não contém elementos.
Modalidades
□	necessariamente	Usado apenas em sistemas de lógica modal. Às vezes, expressa como [] onde o símbolo não está disponível.
◊	possivelmente	Usado apenas em sistemas de lógica modal. Às vezes, expressa como <> onde o símbolo não está disponível.

Propostas, variáveis e símbolos não-lógicos

O uso de variáveis na lógica varia dependendo do sistema e do autor da lógica que está sendo apresentada. No entanto, alguns usos comuns surgiram. Por uma questão de clareza, este site usará o sistema definido abaixo.

Símbolo Significado Notas

A, B, C ... Z proposições Letras em letras maiúsculas significam proposições individuais. Por exemplo, P pode simbolizar a proposição "Pat é ridículo". P e Q são tradicionalmente usados na maioria dos exemplos.

α, β, γ ... ω fórmulas As letras gregas de minúsculas significam fórmulas, que podem ser elas mesmas uma proposição (P), uma fórmula (P ∧ Q) ou várias fórmulas conectadas (φ ∧ ρ).

x, y, z variáveis As letras romanas de minúsculas para o fim do alfabeto são usadas para significar variáveis.Em sistemas lógicos, estes geralmente são acoplados a um quantificador, ∀ ou ∃, para significar alguns ou todos de algum assunto ou objeto não especificado. Por convenção, estes começam com x , mas qualquer outra letra pode ser usada se necessário, desde que sejam definidas como uma variável por um quantificador.

a, b, c, ... z constantes As letras romanas de minúsculas, quando não são atribuídas por um quantificador, significam uma constante, geralmente um substantivo próprio.Por exemplo, a letra "j" pode ser usada para significar "Jerry". As constantes recebem um significado antes de serem usadas em expressões lógicas.

Axe, Bx ... Zx símbolos predicados As letras maiúsculas e latinas aparecem novamente para indicar relações de predicado entre variáveis e / ou constantes, juntamente com um ou mais lugares variáveis que podem ser preenchidos por variáveis ou constantes. Por exemplo, podemos definitiva a relação “x é verde”, como Gx , e “ x gosta y ”, comoLXY . Para diferenciá-los de proposições, eles são frequentemente apresentados em itálico, então, enquanto P pode ser uma proposição, Px é uma relação de predicado para x . Os símbolos de predicação não são lógicos - eles descrevem relações, mas não têm função operacional nem valor de verdade em si mesmos.

Γ, Δ, ... Ω conjuntos de fórmulas As letras gregas maiúsculas são usadas, por convenção, para se referir a conjuntos de fórmulas. Γ geralmente é usado para representar o primeiro site, pois é o primeiro que não se parece com letras romanas. (Por exemplo, o Alfa maiúsculo (Α) parece idêntico à letra romana "A")

Γ, Δ, ... Ω mundos possíveis Na lógica modal , letras maiúsculas maiúsculas também são usadas para representar possíveis mundos.Alternativamente, uma W maiúscula com um número de subíndice às vezes é usada, representando mundos como W ₀ , W ₁ e assim por diante.

{} conjuntos Os suportes encaracolados geralmente são usados ao detalhar o conteúdo de um conjunto, como um conjunto de fórmulas ou um conjunto de mundos possíveis na lógica modal. Por exemplo,Γ = { α, β, γ, δ }

Tabela de símbolos de lógica matemática

Símbolo Nome do símbolo Significado / definição Exemplo

⋅ e e x ⋅ y

^ caret / circumflex e x ^ y

& ampersa e x & y

+ mais ou x + y

∨ caret invertido ou x ∨ y

| Linha vertical ou x | y

x ' citação única não - negação x '

x Barra não - negação x

¬ não não - negação ¬ x

! ponto de exclamação não - negação ! x

⊕ Circular plus / oplus exclusivo ou - xor x ⊕ y

~ til negação ~ x

⇒ implica

⇔ equivalente se e somente se (iff)

↔ equivalente se e somente se (iff)

∀ para todos

∃ existe

∄ não existe

∴ assim sendo

∵

∂

⊥ porque / desde

derivação

Afenque

Esta entre determinado elemento e outro

Nenhum dos dois

Símbolos de cálculo

Cálculo e análise de símbolos e definições de matemática.

Tabela de cálculos e análise de símbolos matemáticos

Símbolo Nome do símbolo Significado / definição Exemplo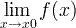

$\ lim_ {x \ para x0} f (x)$ limite valor limite de uma função

ε epsilon representa um número muito pequeno, perto de zero ε → 0

e e constante/ número de Euler e = 2.718281828 ... e = lim (1 + 1 / x) ^x , x → ∞

e ' derivado derivada - notação de Lagrange (3 x ³ ) '= 9 x ²

y '' derivado secundário derivado do derivado (3 x ³ ) '' = 18 x

y ^( n ) n. ° derivado n vezes derivação (3 x ³ )⁽³⁾ = 18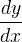

$\ frac {dy} {dx}$ derivado derivado - notação de Leibniz d (3 x ³ ) / dx = 9 x ²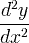

$\ frac {d ^ 2y} {dx ^ 2}$ derivado secundário derivado do derivado d ² (3 x ³) / dx ² = 18 x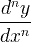

$\ frac {d ^ ny} {dx ^ n}$ n. ° derivado n vezes derivação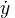

$\ dot {y}$ derivado do tempo derivado por tempo - notação de Newton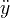

segundo derivado do tempo derivado do derivado

D _xy derivado derivada - notação de Euler

D _x² y derivado secundário derivado do derivado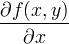

$\ frac {\ parcial f (x, y)} {\ parcial x}$ derivativo parcial ∂ ( x ² +y ² ) / ∂ x= 2 x

∫ integrante oposto à derivação

∬ integral dupla Integração da função de 2 variáveis

∭ integral triplicar Integração da função de 3 variáveis

∮ integral de contorno / linha fechada

∯ integral de superfície fechada

∰ integral de volume fechado

[ a ,b ] intervalo fechado [ a , b ] = { x | a ≤x ≤ b }

( a ,b ) intervalo aberto ( a , b ) = { x | a <x < b }

Eu unidade imaginária eu ≡ √ -1 z = 3 + 2i

z * conjugado complexo z = a + bi→ z * =a - bi z * = 3 + 2 i

z conjugado complexo z = a + bi→ z = a -bi z = 3 + 2i

∇ nabla / del operador de gradiente / divergência ∇ f ( x , y, z )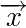

vetor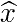

vetor unitário

x y convolução y ( t ) = x( t ) h (t )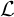

Transformada de Laplace F ( s ) =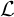{ f ( t )}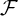

transformada de Fourier X ( ω ) = 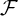{ f ( t)}

δ função delta

∞ lembrancar símbolo infinito

Simbolos de teoria

Lista de símbolos definidos de teoria de conjuntos e probabilidade.

Tabela de símbolos de teoria de conjuntos

Símbolo Nome do símbolo Significado /
definição Exemplo

{} conjunto uma coleção de elementos A = {3,7,9,14},
B = {9,14,28}

| de tal modo que de modo a A = { x |x ∈ 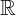$\ mathbb {R}$ , x<0}

A∩B interseção objetos pertencentes ao conjunto A e set B A ∩ B = {9,14}

A∪B União objetos que pertencem ao conjunto A ou conjunto B A ∪ B = {3,7,9,14,28}

A⊆B subconjunto A é um subconjunto de B. o conjunto A está incluído no conjunto B. {9,14,28} ⊆ {9,14,28}

A⊂B subconjunto apropriado / estrito A é um subconjunto de B, mas A não é igual a B. {9,14} ⊂ {9,14,28}

A⊄B não subconjunto definir A não é um subconjunto do conjunto B {9,66} ⊄ {9,14,28}

A⊇B superconjunto A é um superconjunto de B. set A inclui set B {9,14,28} ⊇ {9,14,28}

A⊃B superconjunto próprio / estrito A é um superconjunto de B, mas B não é igual a A. {9,14,28} ⊃ {9,14}

A⊅B não superconjunto definir A não é um superconjunto do conjunto B {9,14,28} ⊅ {9,66}

2 ^A conjunto de força todos os subconjuntos de A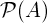

$\ mathcal {P} (A)$ conjunto de força todos os subconjuntos de A

A = B igualdade ambos os conjuntos têm os mesmos membros A = {3,9,14},
B = {3,9,14},
A = B

A ^c complemento todos os objetos que não pertencem ao conjunto A

UMA' complemento todos os objetos que não pertencem ao conjunto A

A \ B complemento relativo objetos que pertencem a A e não a B A = {3,9,14},
B = {1,2,3},
A \ B = {9,14}

AB complemento relativo objetos que pertencem a A e não a B A = {3,9,14},
B = {1,2,3},
A - B = {9,14}

AAB diferença simétrica objetos pertencentes a A ou B, mas não ao seu cruzamento A = {3,9,14},
B = {1,2,3},
A Δ B = {1,2,9,14}

A⊖B diferença simétrica objetos pertencentes a A ou B, mas não ao seu cruzamento A = {3,9,14},
B = {1,2,3},
A ⊖ B = {1,2,9,14}

a ∈ A elemento de conjunto de membros A = {3,9,14}, 3 ∈ A

x ∉A não elemento de nenhuma associação definida A = {3,9,14}, 1 ∉ A

( a ,b ) par ordenado coleção de 2 elementos

A × B produto cartesiano Conjunto de todos os pares ordenados de A e B

| A | cardinalidade o número de elementos do conjunto A A = {3,9,14}, | A | = 3

#UMA cardinalidade o número de elementos do conjunto A A = {3,9,14}, # A = 3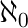

$símbolo$ aleph-null cardinalidade infinita de conjuntos de números naturais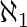

$símbolo$ aleph-one cardinalidade de números ordenáveis contabilizados

Ø conjunto vazio Ø = {} A = Ø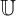

$\ mathbb {U}$ Conjunto universal conjunto de todos os valores possíveis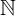

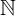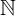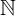$\ mathbb {N}$ ₀ números naturais / números inteiros configurados (com zero) $\ mathbb {N}$ ₀ = {0,1,2,3,4, ...} 0 ∈ $\ mathbb {N}$ ₀

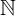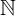$\ mathbb {N}$ ₁ números naturais / números inteiros configurados (sem zero) $\ mathbb {N}$ ₁ = {1,2,3,4,5, ...} 6 ∈ $\ mathbb {N}$ ₁

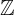
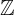$\ mathbb {Z}$ números inteiros configurados $\ mathbb {Z}$ = {...- 3, -2, -1,0,1,2,3, ...} -6 ∈ 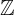$\ mathbb {Z}$

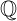
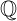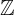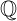
$\ mathbb {Q}$ conjunto de números racionais $\ mathbb {Q}$ = { x |x = a / b ,a , b ∈ $\ mathbb {Z}$ e b ≠ 0} 2/6 ∈ $\ mathbb {Q}$

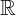
$\ mathbb {R}$ conjunto de números reais 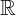$\ mathbb {R}$ = { x |-∞ < x<∞} 6.343434 ∈ 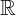$\ mathbb {R}$

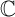
$\ mathbb {C}$ conjunto de números complexos 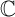$\ mathbb {C}$ = { z |z = a +bi , -∞ <a <∞, -∞ < b <∞} 6 + 2 i ∈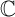 $\ mathbb {C}$

Tabela de símbolos de probabilidade e estatística

Símbolo Nome do símbolo Significado / definição

P ( A ) função de probabilidade probabilidade de evento A

P ( A ∩B ) cruzamento de probabilidade de eventos Probabilidade de eventos A e B

P ( A ∪B ) União de probabilidade de eventos Probabilidade de eventos A ou B

P ( A | B) função de probabilidade condicional Probabilidade de ocorrência Um determinado evento B ocorreu

f ( x ) função de densidade de probabilidade (pdf) P ( a ≤ x ≤ b) = ∫ f ( x )dx

F ( x ) função de distribuição cumulativa (cdf) F ( x ) = P (X ≤ x )

μ média populacional média de valores populacionais

E ( X ) valor de expectativa valor esperado da variável aleatória X

E ( X | Y) expectativa condicional valor esperado da variável aleatória X dado Y

var ( X ) variância variância da variável aleatória X

σ ² variância variância dos valores populacionais

std ( X ) desvio padrão desvio padrão da variável aleatória X

σ _X desvio padrão valor de desvio padrão da variável aleatória X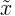

$símbolo mediano$ mediana valor médio da variável aleatória x

cov ( X ,Y ) covariância covariância de variáveis aleatórias X e Y

corr ( X, Y ) correlação correlação das variáveis aleatórias X e Y

ρ _X , Y correlação correlação das variáveis aleatórias X e Y

Σ soma soma - soma de todos os valores na gama de séries

ΣΣ soma dupla soma dupla

Mo modo valor que ocorre mais freqüentemente na população

SR intervalo médio MR = ( x _max + x _min) / 2

Md amostra mediana metade da população está abaixo desse valor

Q ₁ quartil inferior / primeiro 25% da população está abaixo deste valor

Q ₂ mediana / segundo quartil 50% da população está abaixo desse valor = mediana das amostras

Q ₃ quarteto superior / terceiro 75% da população está abaixo desse valor

x média da amostra média / aritmética

s ² variância da amostra Estimador de variância das amostras populacionais

s desvio padrão da amostra estimativa de desvio padrão das amostras populacionais

z _x pontuação padrão z _x = ( x - x) / s _x

X ~ distribuiçãode X distribuição da variável aleatória X

N ( μ , σ ² ) distribuição normal distribuição gaussiana

U ( a , b ) distribuição uniforme probabilidade igual no intervalo a, b

exp (λ) distribuição exponencial f ( x ) = λe ^-λx , x ≥0

gama ( c , λ) distribuição gama f ( x ) = λ cx ^c-1e ^- λx / Γ ( c ), x ≥0

χ ² ( k ) distribuição do qui-quadrado f ( x ) = x ^k^{/ 2-1}e ^{- x / 2} / (2 ^{k / 2} Γ ( k/ 2))

F ( k ₁ , k ₂ ) Distribuição F

Bin ( n , p ) distribuição binomial f ( k ) = _n C _k p ^k (1 -p )^nk

Poisson (λ) Distribuição de veneno f ( k ) = λ ^ke ^- λ / k !

Geom ( p ) distribuição geométrica f ( k ) = p (1-p ) ^k

HG ( N , K ,n ) distribuição hiper-geométrica

Berna ( p ) Distribuição de Bernoulli

Pesquisar este blog

A Manifestação do espírito-racional

LÓGICA: SÍMBOLOS

Símbolos de lógica

Comentários

Postar um comentário

Postagens mais visitadas

LÓGICA QUANTICA: UMA INTRODUÇÃO

SCHELLING: UMA INTRODUÇÃO

Símbolo	Significado	Notas
A, B, C ... Z	proposições	Letras em letras maiúsculas significam proposições individuais. Por exemplo, P pode simbolizar a proposição "Pat é ridículo". P e Q são tradicionalmente usados na maioria dos exemplos.
α, β, γ ... ω	fórmulas	As letras gregas de minúsculas significam fórmulas, que podem ser elas mesmas uma proposição (P), uma fórmula (P ∧ Q) ou várias fórmulas conectadas (φ ∧ ρ).
x, y, z	variáveis	As letras romanas de minúsculas para o fim do alfabeto são usadas para significar variáveis.Em sistemas lógicos, estes geralmente são acoplados a um quantificador, ∀ ou ∃, para significar alguns ou todos de algum assunto ou objeto não especificado. Por convenção, estes começam com x , mas qualquer outra letra pode ser usada se necessário, desde que sejam definidas como uma variável por um quantificador.
a, b, c, ... z	constantes	As letras romanas de minúsculas, quando não são atribuídas por um quantificador, significam uma constante, geralmente um substantivo próprio.Por exemplo, a letra "j" pode ser usada para significar "Jerry". As constantes recebem um significado antes de serem usadas em expressões lógicas.
Axe, Bx ... Zx	símbolos predicados	As letras maiúsculas e latinas aparecem novamente para indicar relações de predicado entre variáveis e / ou constantes, juntamente com um ou mais lugares variáveis que podem ser preenchidos por variáveis ou constantes. Por exemplo, podemos definitiva a relação “x é verde”, como Gx , e “ x gosta y ”, comoLXY . Para diferenciá-los de proposições, eles são frequentemente apresentados em itálico, então, enquanto P pode ser uma proposição, Px é uma relação de predicado para x . Os símbolos de predicação não são lógicos - eles descrevem relações, mas não têm função operacional nem valor de verdade em si mesmos.
Γ, Δ, ... Ω	conjuntos de fórmulas	As letras gregas maiúsculas são usadas, por convenção, para se referir a conjuntos de fórmulas. Γ geralmente é usado para representar o primeiro site, pois é o primeiro que não se parece com letras romanas. (Por exemplo, o Alfa maiúsculo (Α) parece idêntico à letra romana "A")
Γ, Δ, ... Ω	mundos possíveis	Na lógica modal , letras maiúsculas maiúsculas também são usadas para representar possíveis mundos.Alternativamente, uma W maiúscula com um número de subíndice às vezes é usada, representando mundos como W ₀ , W ₁ e assim por diante.
{}	conjuntos	Os suportes encaracolados geralmente são usados ao detalhar o conteúdo de um conjunto, como um conjunto de fórmulas ou um conjunto de mundos possíveis na lógica modal. Por exemplo,Γ = { α, β, γ, δ }

Símbolo	Nome do símbolo	Significado / definição	Exemplo
⋅	e	e	x ⋅ y
^	caret / circumflex	e	x ^ y
&	ampersa	e	x & y
+	mais	ou	x + y
∨	caret invertido	ou	x ∨ y
\|	Linha vertical	ou	x \| y
x '	citação única	não - negação	x '
x	Barra	não - negação	x
¬	não	não - negação	¬ x
!	ponto de exclamação	não - negação	! x
⊕	Circular plus / oplus	exclusivo ou - xor	x ⊕ y
~	til	negação	~ x
⇒	implica
⇔	equivalente	se e somente se (iff)
↔	equivalente	se e somente se (iff)
∀	para todos
∃	existe
∄	não existe
∴	assim sendo
∵ ∂ ⊥	porque / desde derivação Afenque	Esta entre determinado elemento e outro Nenhum dos dois

Símbolo	Nome do símbolo	Significado / definição	Exemplo
$\ lim_ {x \ para x0} f (x)$	limite	valor limite de uma função
ε	epsilon	representa um número muito pequeno, perto de zero	ε → 0
e	e constante/ número de Euler	e = 2.718281828 ...	e = lim (1 + 1 / x) ^x , x → ∞
e '	derivado	derivada - notação de Lagrange	(3 x ³ ) '= 9 x ²
y ''	derivado secundário	derivado do derivado	(3 x ³ ) '' = 18 x
y ^( n )	n. ° derivado	n vezes derivação	(3 x ³ )⁽³⁾ = 18
$\ frac {dy} {dx}$	derivado	derivado - notação de Leibniz	d (3 x ³ ) / dx = 9 x ²
$\ frac {d ^ 2y} {dx ^ 2}$	derivado secundário	derivado do derivado	d ² (3 x ³) / dx ² = 18 x
$\ frac {d ^ ny} {dx ^ n}$	n. ° derivado	n vezes derivação
$\ dot {y}$	derivado do tempo	derivado por tempo - notação de Newton
	segundo derivado do tempo	derivado do derivado
D _xy	derivado	derivada - notação de Euler
D _x² y	derivado secundário	derivado do derivado
$\ frac {\ parcial f (x, y)} {\ parcial x}$	derivativo parcial		∂ ( x ² +y ² ) / ∂ x= 2 x
∫	integrante	oposto à derivação
∬	integral dupla	Integração da função de 2 variáveis
∭	integral triplicar	Integração da função de 3 variáveis
∮	integral de contorno / linha fechada
∯	integral de superfície fechada
∰	integral de volume fechado
[ a ,b ]	intervalo fechado	[ a , b ] = { x \| a ≤x ≤ b }
( a ,b )	intervalo aberto	( a , b ) = { x \| a <x < b }
Eu	unidade imaginária	eu ≡ √ -1	z = 3 + 2i
z *	conjugado complexo	z = a + bi→ z * =a - bi	z * = 3 + 2 i
z	conjugado complexo	z = a + bi→ z = a -bi	z = 3 + 2i
∇	nabla / del	operador de gradiente / divergência	∇ f ( x , y, z )
	vetor
	vetor unitário
x *y	convolução	y ( t ) = x( t ) * h (t )
	Transformada de Laplace	F ( s ) ={ f ( t )}
	transformada de Fourier	X ( ω ) = { f ( t)}
δ	função delta
∞	lembrancar	símbolo infinito

Símbolo	Nome do símbolo	Significado / definição	Exemplo
{}	conjunto	uma coleção de elementos	A = {3,7,9,14}, B = {9,14,28}
\|	de tal modo que	de modo a	A = { x \|x ∈ $\ mathbb {R}$ , x<0}
A∩B	interseção	objetos pertencentes ao conjunto A e set B	A ∩ B = {9,14}
A∪B	União	objetos que pertencem ao conjunto A ou conjunto B	A ∪ B = {3,7,9,14,28}
A⊆B	subconjunto	A é um subconjunto de B. o conjunto A está incluído no conjunto B.	{9,14,28} ⊆ {9,14,28}
A⊂B	subconjunto apropriado / estrito	A é um subconjunto de B, mas A não é igual a B.	{9,14} ⊂ {9,14,28}
A⊄B	não subconjunto	definir A não é um subconjunto do conjunto B	{9,66} ⊄ {9,14,28}
A⊇B	superconjunto	A é um superconjunto de B. set A inclui set B	{9,14,28} ⊇ {9,14,28}
A⊃B	superconjunto próprio / estrito	A é um superconjunto de B, mas B não é igual a A.	{9,14,28} ⊃ {9,14}
A⊅B	não superconjunto	definir A não é um superconjunto do conjunto B	{9,14,28} ⊅ {9,66}
2 ^A	conjunto de força	todos os subconjuntos de A
$\ mathcal {P} (A)$	conjunto de força	todos os subconjuntos de A
A = B	igualdade	ambos os conjuntos têm os mesmos membros	A = {3,9,14}, B = {3,9,14}, A = B
A ^c	complemento	todos os objetos que não pertencem ao conjunto A
UMA'	complemento	todos os objetos que não pertencem ao conjunto A
A \ B	complemento relativo	objetos que pertencem a A e não a B	A = {3,9,14}, B = {1,2,3}, A \ B = {9,14}
AB	complemento relativo	objetos que pertencem a A e não a B	A = {3,9,14}, B = {1,2,3}, A - B = {9,14}
AAB	diferença simétrica	objetos pertencentes a A ou B, mas não ao seu cruzamento	A = {3,9,14}, B = {1,2,3}, A Δ B = {1,2,9,14}
A⊖B	diferença simétrica	objetos pertencentes a A ou B, mas não ao seu cruzamento	A = {3,9,14}, B = {1,2,3}, A ⊖ B = {1,2,9,14}
a ∈ A	elemento de	conjunto de membros	A = {3,9,14}, 3 ∈ A
x ∉A	não elemento de	nenhuma associação definida	A = {3,9,14}, 1 ∉ A
( a ,b )	par ordenado	coleção de 2 elementos
A × B	produto cartesiano	Conjunto de todos os pares ordenados de A e B
\| A \|	cardinalidade	o número de elementos do conjunto A	A = {3,9,14}, \| A \| = 3
#UMA	cardinalidade	o número de elementos do conjunto A	A = {3,9,14}, # A = 3
$símbolo$	aleph-null	cardinalidade infinita de conjuntos de números naturais
$símbolo$	aleph-one	cardinalidade de números ordenáveis contabilizados
Ø	conjunto vazio	Ø = {}	A = Ø
$\ mathbb {U}$	Conjunto universal	conjunto de todos os valores possíveis
$\ mathbb {N}$ ₀	números naturais / números inteiros configurados (com zero)	$\ mathbb {N}$ ₀ = {0,1,2,3,4, ...}	0 ∈ $\ mathbb {N}$ ₀
$\ mathbb {N}$ ₁	números naturais / números inteiros configurados (sem zero)	$\ mathbb {N}$ ₁ = {1,2,3,4,5, ...}	6 ∈ $\ mathbb {N}$ ₁
$\ mathbb {Z}$	números inteiros configurados	$\ mathbb {Z}$ = {...- 3, -2, -1,0,1,2,3, ...}	-6 ∈ $\ mathbb {Z}$
$\ mathbb {Q}$	conjunto de números racionais	$\ mathbb {Q}$ = { x \|x = a / b ,a , b ∈ $\ mathbb {Z}$ e b ≠ 0}	2/6 ∈ $\ mathbb {Q}$
$\ mathbb {R}$	conjunto de números reais	$\ mathbb {R}$ = { x \|-∞ < x<∞}	6.343434 ∈ $\ mathbb {R}$
$\ mathbb {C}$	conjunto de números complexos	$\ mathbb {C}$ = { z \|z = a +bi , -∞ <a <∞, -∞ < b <∞}	6 + 2 i ∈ $\ mathbb {C}$

Símbolo	Nome do símbolo	Significado / definição
P ( A )	função de probabilidade	probabilidade de evento A
P ( A ∩B )	cruzamento de probabilidade de eventos	Probabilidade de eventos A e B
P ( A ∪B )	União de probabilidade de eventos	Probabilidade de eventos A ou B
P ( A \| B)	função de probabilidade condicional	Probabilidade de ocorrência Um determinado evento B ocorreu
f ( x )	função de densidade de probabilidade (pdf)	P ( a ≤ x ≤ b) = ∫ f ( x )dx
F ( x )	função de distribuição cumulativa (cdf)	F ( x ) = P (X ≤ x )
μ	média populacional	média de valores populacionais
E ( X )	valor de expectativa	valor esperado da variável aleatória X
E ( X \| Y)	expectativa condicional	valor esperado da variável aleatória X dado Y
var ( X )	variância	variância da variável aleatória X
σ ²	variância	variância dos valores populacionais
std ( X )	desvio padrão	desvio padrão da variável aleatória X
σ _X	desvio padrão	valor de desvio padrão da variável aleatória X
$símbolo mediano$	mediana	valor médio da variável aleatória x
cov ( X ,Y )	covariância	covariância de variáveis aleatórias X e Y
corr ( X, Y )	correlação	correlação das variáveis aleatórias X e Y
ρ _X , Y	correlação	correlação das variáveis aleatórias X e Y
Σ	soma	soma - soma de todos os valores na gama de séries
ΣΣ	soma dupla	soma dupla
Mo	modo	valor que ocorre mais freqüentemente na população
SR	intervalo médio	MR = ( x _max + x _min) / 2
Md	amostra mediana	metade da população está abaixo desse valor
Q ₁	quartil inferior / primeiro	25% da população está abaixo deste valor
Q ₂	mediana / segundo quartil	50% da população está abaixo desse valor = mediana das amostras
Q ₃	quarteto superior / terceiro	75% da população está abaixo desse valor
x	média da amostra	média / aritmética
s ²	variância da amostra	Estimador de variância das amostras populacionais
s	desvio padrão da amostra	estimativa de desvio padrão das amostras populacionais
z _x	pontuação padrão	z _x = ( x - x) / s _x
X ~	distribuiçãode X	distribuição da variável aleatória X
N ( μ , σ ² )	distribuição normal	distribuição gaussiana
U ( a , b )	distribuição uniforme	probabilidade igual no intervalo a, b
exp (λ)	distribuição exponencial	f ( x ) = λe ^-λx , x ≥0
gama ( c , λ)	distribuição gama	f ( x ) = λ cx ^c-1e ^- λx / Γ ( c ), x ≥0
χ ² ( k )	distribuição do qui-quadrado	f ( x ) = x ^k^{/ 2-1}e ^{- x / 2} / (2 ^{k / 2} Γ ( k/ 2))
F ( k ₁ , k ₂ )	Distribuição F
Bin ( n , p )	distribuição binomial	f ( k ) = _n C _k p ^k (1 -p )^nk
Poisson (λ)	Distribuição de veneno	f ( k ) = λ ^ke ^- λ / k !
Geom ( p )	distribuição geométrica	f ( k ) = p (1-p ) ^k
HG ( N , K ,n )	distribuição hiper-geométrica
Berna ( p )	Distribuição de Bernoulli